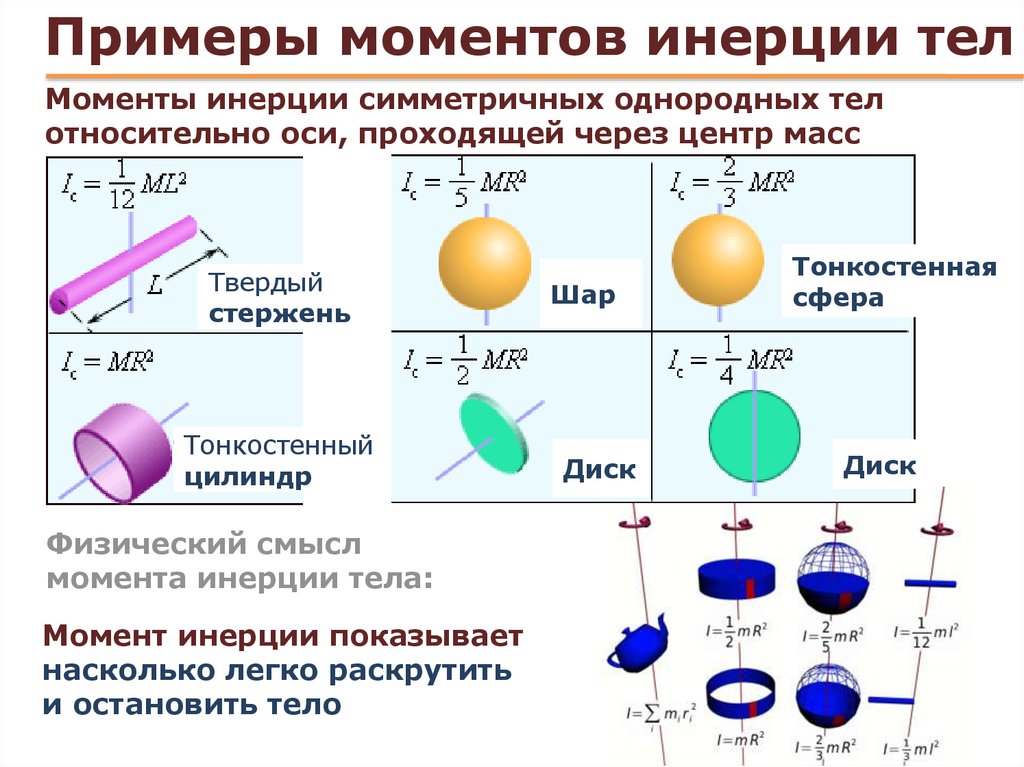
6.3. Момент инерции простейших симметричных тел
Из определения момента инерции системы материальных точек следует, что при вычислении момента инерции сплошного тела массу mi материальной точки следует заменить массой элемента тела dm, а суммирование – интегрированием, так что
а учитывая, что dm = 𝜌dV, где dV – элемент объема тела, 𝜌 – плотность материала тела,
(6.11)
В случае симметричных тел момент инерции с помощью этой формулы вычисляется легко. Вычислим в качестве примера момент инерции двух симметричных тел.
Момент инерции стержня относительно оси, проходящей через его центр.
Представим себе
стержень длины l площадью поперечного сечения S и массы m. Направим вдоль стержня координатную
ось
Направим вдоль стержня координатную
ось
При получении конечного выражения, было учтено, что 𝜌Sl = m – масса стержня.
Момент инерции однородного диска относительно оси, проходящей через его центр.
Воспользуемся формулой (6.11) в цилиндрической системе координат, в которой элемент объема
Поскольку масса диска m = 𝜌𝜋R2h, получим
Приведем без
вычисления осевые моменты инерции
других однородных тел простейшей
геометрической формы, которые рассчитаны
относительно оси, проходящей через
центр масс.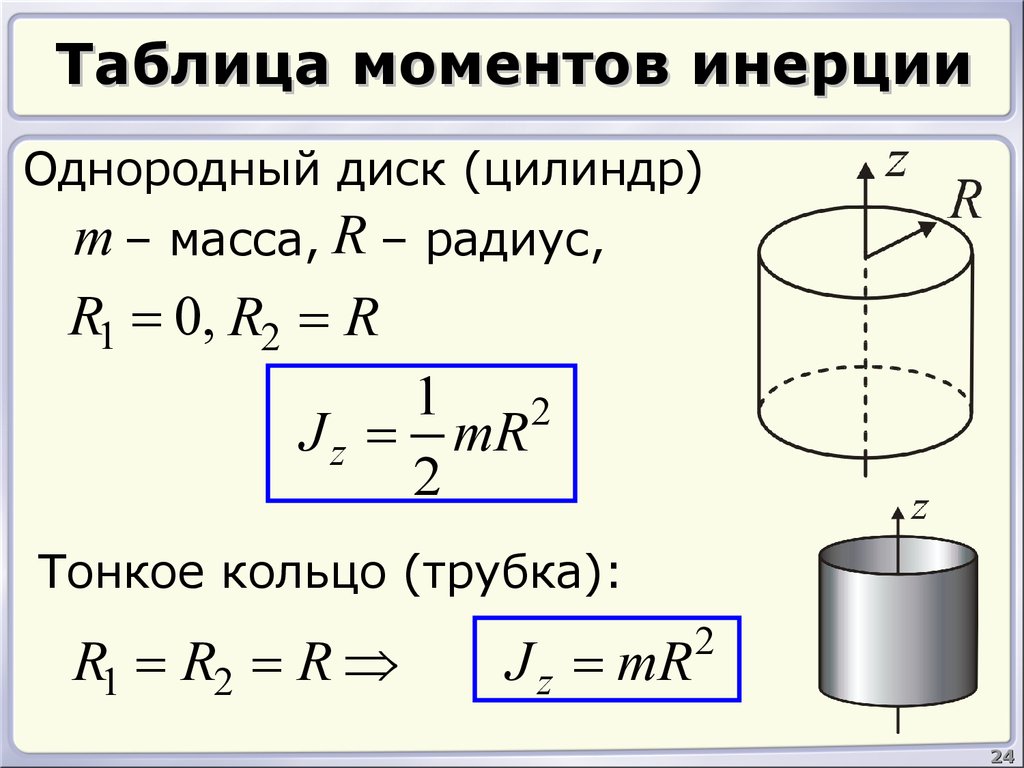
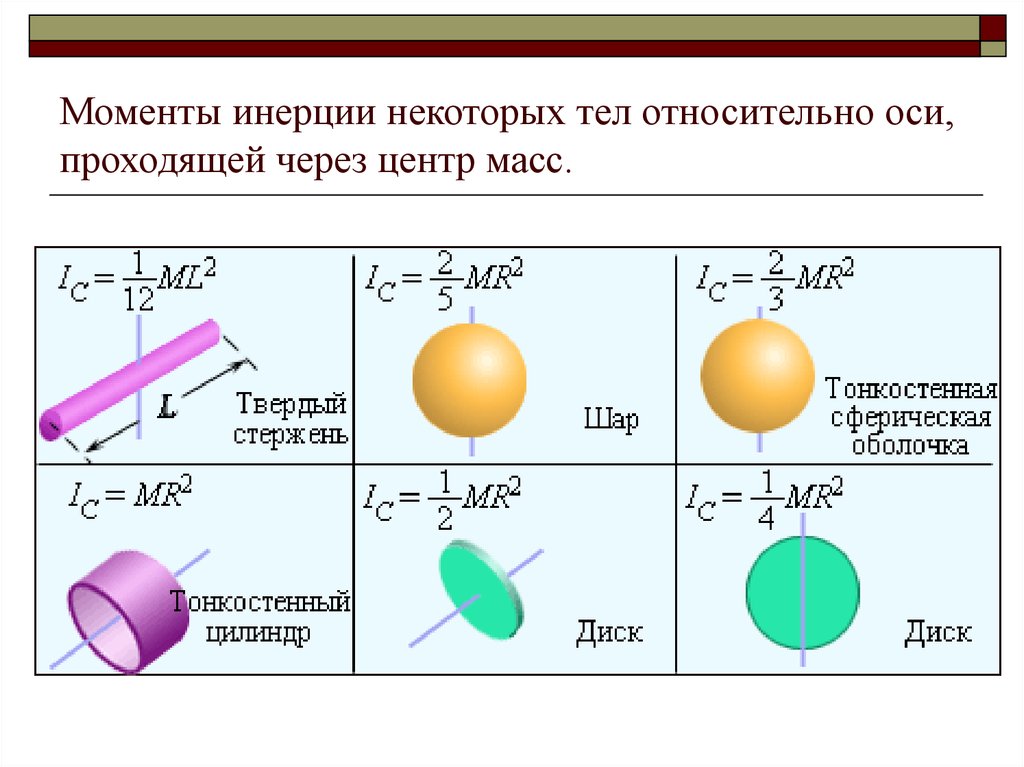
Момент инерции сплошного цилиндра радиусом R относительно его оси:
Момент инерции толстостенного цилиндра относительно его оси:
где R1 и R2 – его внутренний и внешний радиусы соответственно.
Момент инерции тонкостенного цилиндра (R1 = R2 = R) относительно оси:
Момент инерции однородного шара радиусом R относительно оси, проходящей через его центр:
Моменты инерции тел сложной формы определяются экспериментально.
Предположим
теперь, что нам известен момент инерции
тела относительно оси ОО,
проходящей через центр инерции тела С,
и требуется найти момент инерции тела
относительно оси О1О1,
параллельной ОО и находящейся на расстоянии а от нее (рис. 6.). Мысленно разобьем тело
на отдельные элементы массой dm и обозначим через r0 расстояние от этого элемента до оси ОО,
а через r – его расстояние до оси ОО
6.). Мысленно разобьем тело
на отдельные элементы массой dm и обозначим через r0 расстояние от этого элемента до оси ОО,
а через r – его расстояние до оси ОО
Умножим обе части этого равенства на и проинтегрируем по всему объему тела, получим
Здесь первый интеграл в правой части второго равенства определяет момент инерции I0 тела относительно оси ОО, проходящей через центр инерции, второй интеграл равен
Рис. 6 |
Для вычисления третьего интеграла расположим в плоскости, проходящей через оси ОО и О1
 Тогда, как видно из рис. 6, – x-координата
центра элемента dm.
Следовательно, Эта величина согласно (4.**) равна ,
где xC – x-координата
центра инерции С. А
поскольку то равен нулю и третий интеграл. В итоге
получим
Тогда, как видно из рис. 6, – x-координата
центра элемента dm.
Следовательно, Эта величина согласно (4.**) равна ,
где xC – x-координата
центра инерции С. А
поскольку то равен нулю и третий интеграл. В итоге
получимТаким образом, момент инерции тела относительно любой оси равен сумме момента инерции относительно оси, проходящей через центр инерции и величины, равной произведению массы тела на квадрат расстояния между осями. Это утверждение и составляет содержание теоремы Штейнера. В качестве примера применения теоремы Штейнера найдем момент инерции стержня относительно оси, проходящей через один из его концов. В данном случае
Курс теоретической механики
Курс теоретической механики
ОглавлениеПредисловиеВведение § 1. СВОБОДНЫЕ ВЕКТОРЫ 2. Сложение свободных векторов. 3. Проекция вектора на ось. 4. Инварианты системы свободных векторов. § 2. СКОЛЬЗЯЩИЕ ВЕКТОРЫ 2. Координаты скользящего вектора. 3. Момент скользящего вектора. Плюккеровы координаты.  4. Аналитическое определение момента скользящего вектора. 5. Проекция момента на ось. 6. Момент скользящего вектора относительно оси § 3. СИСТЕМА СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Произвольная система скользящих векторов. Элементарные операции. 3. Приведение системы скользящих векторов к простейшей эквивалентной форме. 5. Свойства системы параллельных скользящих векторов. § 4. ЗАКРЕПЛЕННЫЕ ВЕКТОРЫ § 5. ДИФФЕРЕНЦИРОВАНИЕ СВОБОДНОГО ВЕКТОРА ПО СКАЛЯРНОМУ АРГУМЕНТУ Глава II. КИНЕМАТИКА § 1. КИНЕМАТИКА ТОЧКИ 2. Ускорение точки. Проекции ускорения на прямоугольные оси координат. 3. Скорость и ускорение точки в полярных координатах. 4. Движение точки по окружности. 5. Проекции ускорения на оси естественного трехгранника. 6. Теорема о сложении скоростей в сложном движении точки. 7. Метод Роберваля построения касательных к плоским кривым. 8. Аналитическое доказательство теоремы о сложении скоростей.  9. Сложение скоростей в общем случае сложного движения точки. § 2. КИНЕМАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА 2. Элементарные движения твердого тела. 3. Мгновенные движения твердого тела. 4. Сложение мгновенно-поступательных и мгновенно-вращательных движений твердого тела. 5. Общий случай сложения мгновенно-поступательных и мгновенно-вращательных движений твердого тела. Непрерывное движение твердого тела. 6. Мгновенное движение твердого тела с одной неподвижной точкой. 7. Плоскопараллельное движение твердого тела. § 3. УСКОРЕНИЕ ТОЧКИ В СЛОЖНОМ ДВИЖЕНИИ 2. Замечание о дифференцировании единичного вектора. 4. Теорема Ривальса. § 4. РАСПРЕДЕЛЕНИЕ УСКОРЕНИЙ В ПЛОСКОПАРАЛЛЕЛЬНОМ ДВИЖЕНИИ ТВЕРДОГО ТЕЛА 2. Мгновенный центр ускорений. § 5. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ЭЙЛЕРА Глава III. СТАТИКА I. ГЕОМЕТРИЧЕСКАЯ СТАТИКА § 1. АКСИОМЫ СТАТИКИ § 2. ПОНЯТИЕ О СИЛЕ ТРЕНИЯ § 3. РАЗЛИЧНЫЕ ЗАДАЧИ СТАТИКИ 2.  Равновесие трех сил. Равновесие трех сил.§ 4. МОМЕНТ СИЛЫ 2. Момент силы относительно оси. 3. Теорема Вариньона для системы сходящихся сил. § 5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО § 6. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ СИЛ, ДЕЙСТВУЮЩИХ НА ТВЕРДОЕ ТЕЛО § 8. УСЛОВИЯ РАВНОВЕСИЯ СИСТЕМЫ ТВЕРДЫХ ТЕЛ § 9. ПЛОСКАЯ СИСТЕМА СИЛ § 10. ЗАДАЧА О РАВНОВЕСИИ НЕСВОБОДНОГО ТВЕРДОГО ТЕЛА 2. Частные случаи равновесия твердого тела. § 11. ЗАДАЧА О РАВНОВЕСИИ ПРИ НАЛИЧИИ ТРЕНИЯ § 12. СИЛА ТЯЖЕСТИ И ЦЕНТР ТЯЖЕСТИ II. АНАЛИТИЧЕСКАЯ СТАТИКА § 1. РАБОТА СИЛЫ НА ПЕРЕМЕЩЕНИИ. СИЛОВАЯ ФУНКЦИЯ § 2. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 2. Теорема Лагранжа о равновесии системы. 3. Принцип Торричелли. § 3. ОБЩИЕ ВОПРОСЫ АНАЛИТИЧЕСКОЙ СТАТИКИ 3. Общие теоремы о равновесии системы материальных точек. 4. Метод неопределенных множителей Лагранжа. 5. Определение реакций.  § 4. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОБЩЕМ СЛУЧАЕ § 5. РАВНОВЕСИЕ НИТИ 2. Естественные уравнения равновесия нити. Глава IV. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ § 1. ОСНОВНЫЕ ЗАКОНЫ ДИНАМИКИ § 2. ДВЕ ОСНОВНЫЕ ЗАДАЧИ ДИНАМИКИ. УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В ДЕКАРТОВЫХ ОСЯХ § 3. ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ § 4. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ ДЛЯ СВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 2. Теорема об изменении момента количества движения. 3. Следствия из теорем об изменении количества движения и момента количества движения материальной точки. 4. Теорема живых сил. 5. Интеграл живых сил. 6. Устойчивость равновесия. Теорема Лагранжа. § 5. ДВИЖЕНИЕ ТЯЖЕЛОЙ МАТЕРИАЛЬНОЙ ТОЧКИ В ПУСТОТЕ § 6. ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНЫХ СИЛ 2. Формулы Бине 3. Задача о движении планет § 7. ДВИЖЕНИЕ ТОЧКИ В СОПРОТИВЛЯЮЩЕЙСЯ СРЕДЕ § 8. ДВИЖЕНИЕ НЕСВОБОДНОЙ МАТЕРИАЛЬНОЙ ТОЧКИ 2. Движение материальной точки по поверхности. § 9. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 1. 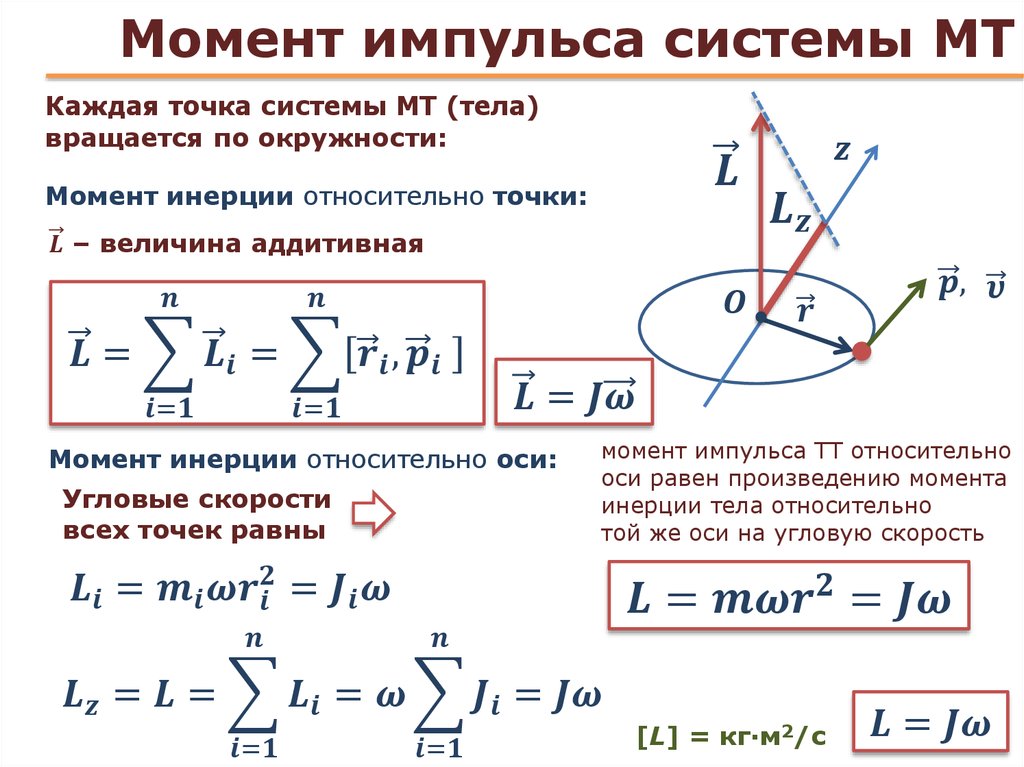 Теорема живых сил в относительном движении точки. Теорема живых сил в относительном движении точки.2. Уравнения относительного равновесия точки. 3. Равновесие материальной точки на поверхности Земли. Вес. 4. Задача о падении тяжелой точки в пустоте. 5. Маятник Фуко. § 10. ПРИНЦИП ДАЛАМБЕРА Глава V. ДИНАМИКА СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК § 1. УЧЕНИЕ О СВЯЗЯХ § 2. ПРИНЦИП ДАЛАМБЕРА – ЛАГРАНЖА § 3. ОСНОВНЫЕ ТЕОРЕМЫ ДИНАМИКИ СИСТЕМЫ 2. Теорема об изменении момента количества движения. 3. Теорема живых сил. § 4. ТЕОРЕМЫ О ДВИЖЕНИИ СИСТЕМЫ ОТНОСИТЕЛЬНО ОСЕЙ НЕИЗМЕННОГО НАПРАВЛЕНИЯ, ПРОХОДЯЩИХ ЧЕРЕЗ ЦЕНТР МАСС СИСТЕМЫ (ОСЕЙ КЕНИГА) 2. Теорема об изменении момента количества движения системы относительно осей Кёнига. 3. Теорема живых сил в движении системы относительно осей Кёнига. § 5. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА 2. Случай существования силовой функции. 3. Замечание о лагранжевых координатах. § 6. ЭЛЕМЕНТАРНЫЕ СЛУЧАИ ИНТЕГРИРУЕМОСТИ УРАВНЕНИЙ ЛАГРАНЖА 2. Метод Рауса игнорирования циклических координат.  3. Обобщение теоремы и интеграла живых сил. § 7. ОПРЕДЕЛЕНИЕ РЕАКЦИЙ Глава VI. ДИНАМИКА ТВЕРДОГО ТЕЛА § 1. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ 2. Момент инерции системы относительно произвольной оси, проходящей через заданную точку. 3. Эллипсоид инерции. 4. Определение главных осей инерции для произвольной точки. § 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ОСИ § 3. ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА, ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ 2. Уравнения движения твердого тела с одной неподвижной точкой. § 4. ДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ 2. Интегрирование уравнений движения тяжелого твердого тела. 3. Случай Эйлера — Пуансо. Регулярная прецессия твердого тела в случае Эйлера. Геометрическая интерпретация Пуансо движения твердого тела в случае Эйлера. Устойчивость постоянных вращений твердого тела. 4. Случай Лагранжа. Особенные случаи движения твердого тела. Спящий волчок. Гироскоп. Приближенная теория. Некоторые применения гироскопов.  Регулярная прецессия в случае Лагранжа. Вынужденная регулярная прецессия. 5. Случай Ковалевской. § 5. ОПРЕДЕЛЕНИЕ РЕАКЦИИ В СЛУЧАЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ § 6. УРАВНЕНИЯ ДВИЖЕНИЯ СВОБОДНОГО ТВЕРДОГО ТЕЛА § 7. ГИРОСТАТЫ Глава VII. АНАЛИТИЧЕСКАЯ ДИНАМИКА § 1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА 1. Преобразования Лежандра. 2. Канонические уравнения Гамильтона. 3. Функция Гамильтона и ее свойства. § 2. ПРИНЦИП ГАМИЛЬТОНА – ОСТРОГРАДСКОГО 2. Вывод канонических уравнений Гамильтона из принципа Гамильтона — Остроградского. 3. Принцип Гамильтона в форме Пуанкаре. § 3. ИНТЕГРИРОВАНИЕ КАНОНИЧЕСКИХ УРАВНЕНИЙ ГАМИЛЬТОНА 2. Канонические преобразования. 3. Бесконечно малые канонические преобразования. 4. Теорема Лиувилля. 5. Теорема Якоби. 6. Интегрирование уравнения Гамильтона—Якоби. Метод Имшенецкого разделения переменных. 7. Скобки Пуассона. § 4. ВАРИАЦИОННЫЕ ПРИНЦИПЫ МЕХАНИКИ 2.  Принцип Лагранжа. Принцип Лагранжа.3. Принцип наименьшего действия в форме Якоби. Вывод уравнений Лагранжа второго рода из принципа Якоби. Сравнение принципа Якоби с принципом Гамильтона. 4. Оптико-механическая аналогия. 5. Интегральные инварианты. Линейные интегральные инварианты. Интегральный инвариант Пуанкаре — Картана. 6. Принцип наименьшего принуждения Гаусса. Уравнения Аппеля. 7. Уравнения Рауса. § 5. МАЛЫЕ КОЛЕБАНИЯ Затухающие колебания. Вынужденные колебания. Резонанс. Параметрический резонанс. Нелинейные колебания. Диссипативные системы. 2. Общий случай малых колебаний системы около положения устойчивого равновесия. Устойчивость равновесия. Теорема Лагранжа об устойчивости равновесия. Замечание об устойчивости стационарных движений. Малые колебания системы около положения устойчивого равновесия. Влияние диссипативных сил на малые колебания системы около устойчивого положения равновесия. § 6. УСТОЙЧИВОСТЬ ДВИЖЕНИЯ Прямой метод Ляпунова Теорема об асимптотической устойчивости.  Теорема Четаева о неустойчивости движения. 2. Влияние новых связей на малые колебания системы около положения равновесия. 3. Влияние диссипативных сил на устойчивость равновесия. 4. Влияние гироскопических сил на устойчивость равновесия. § 7. ЭЛЕМЕНТЫ ТЕОРИИ ВОЗМУЩЕНИЙ Устойчивость консервативных систем. 2. Метод изменения произвольных постоянных. Глава VIII. ТЕОРИЯ УДАРА § 2. ТЕОРЕМЫ КАРНО § 3. ЗАДАЧА О ЦЕНТРЕ УДАРА § 4. ЗАДАЧА О БАЛЛИСТИЧЕСКОМ МАЯТНИКЕ § 5. УРАВНЕНИЯ ЛАГРАНЖА ДЛЯ УДАРА § 6. ЗАДАЧА ОБ УДАРЕ ПО ТВЕРДОМУ ТЕЛУ С ОДНОЙ НЕПОДВИЖНОЙ ТОЧКОЙ Глава IX. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. СПЕЦИАЛЬНЫЙ ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА § 3. ГРУППА ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА § 4. ИНВАРИАНТНЫЕ ВЕЛИЧИНЫ В ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ЧЕТЫРЕХМЕРНЫЙ ВЕКТОР. МИР МИНКОВСКОГО § 5. РЕЛЯТИВИСТСКАЯ ДИНАМИКА Литература |
Карта механики — Теорема о параллельных осях
В качестве альтернативы интегрированию моменты инерции площади и массы могут быть рассчитаны с помощью метода составных частей, подобно тому, как мы это делали с центроидами. В этом методе мы будем разбивать сложную форму на простые части, искать моменты инерции для этих частей в таблице, корректировать моменты инерции для положения и, наконец, складывать скорректированные значения вместе, чтобы найти общий момент инерции. Этот метод известен как метод составных частей .
В этом методе мы будем разбивать сложную форму на простые части, искать моменты инерции для этих частей в таблице, корректировать моменты инерции для положения и, наконец, складывать скорректированные значения вместе, чтобы найти общий момент инерции. Этот метод известен как метод составных частей .
Ключевой частью этого процесса, которой не было в расчетах центроидов, является корректировка положения. Как обсуждалось на предыдущих страницах, площадь и моменты инерции масс зависят от выбранной оси вращения. Моменты инерции частей тела могут складываться только тогда, когда они взяты относительно одной и той же оси . Однако моменты инерции в таблице обычно указаны относительно центроида этой формы. Поскольку каждая часть имеет свою собственную координату центра тяжести, мы не можем просто сложить эти числа. Мы будем использовать что-то под названием Параллельная ось Теорема , чтобы настроить моменты инерции так, чтобы все они были взяты относительно некоторой стандартной оси или точки. Как только моменты инерции будут скорректированы с помощью теоремы о параллельных осях, мы можем сложить их вместе, используя метод составных частей.
Как только моменты инерции будут скорректированы с помощью теоремы о параллельных осях, мы можем сложить их вместе, используя метод составных частей.
Теорема о параллельных осях
Когда мы вычисляли момент инерции площади и массы с помощью интегрирования, одной из первых вещей, которые нам нужно было сделать, было выбрать точку или ось, относительно которой мы собирались измерять момент инерции. Затем мы измерили все расстояния от этой точки или оси, где расстояния были плечами моментов в наших интегралах моментов. Поскольку центр тяжести фигуры является геометрическим центром площади или объема, среднее расстояние до любой точки тела минимально. Если мы выберем другую точку или ось для измерения момента инерции, то в среднем все расстояния в нашем интеграле моментов будут немного больше. В частности, чем дальше мы удаляемся от центроида, тем больше становятся средние расстояния.
Расстояния, используемые в наших интегралах моментов, зависят от выбранной точки или оси.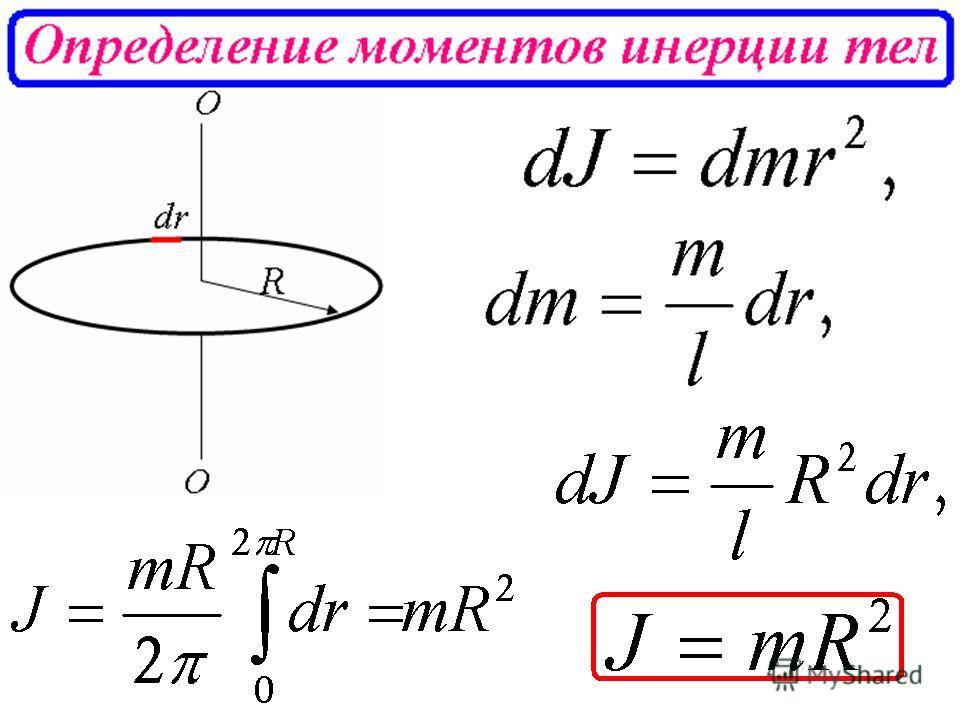 Эти расстояния будут минимальными в центроиде и будут увеличиваться по мере того, как мы начинаем дальше от центроида.
Эти расстояния будут минимальными в центроиде и будут увеличиваться по мере того, как мы начинаем дальше от центроида.Хотя это усложняет наш анализ, приятно то, что изменение момента инерции предсказуемо. Он всегда будет минимальным, если мы возьмем момент инерции относительно центроида или оси, проходящей через центроид (площадной момент инерции), и минимальным относительно оси, проходящей через центр тяжести (массовый момент инерции). Этот минимум, который мы будем называть I 9{2}\]
Этот процесс настройки с приведенными выше уравнениями является теоремой о параллельной оси . Термины площади или массы просто представляют собой площадь или массу части, на которую вы смотрите, в то время как расстояние (r) представляет собой расстояние, на которое мы перемещаем ось, вокруг которой мы измеряем момент инерции. Это может быть расстояние по вертикали, расстояние по горизонтали или диагональ в зависимости от оси, вокруг которой находится момент или инерция.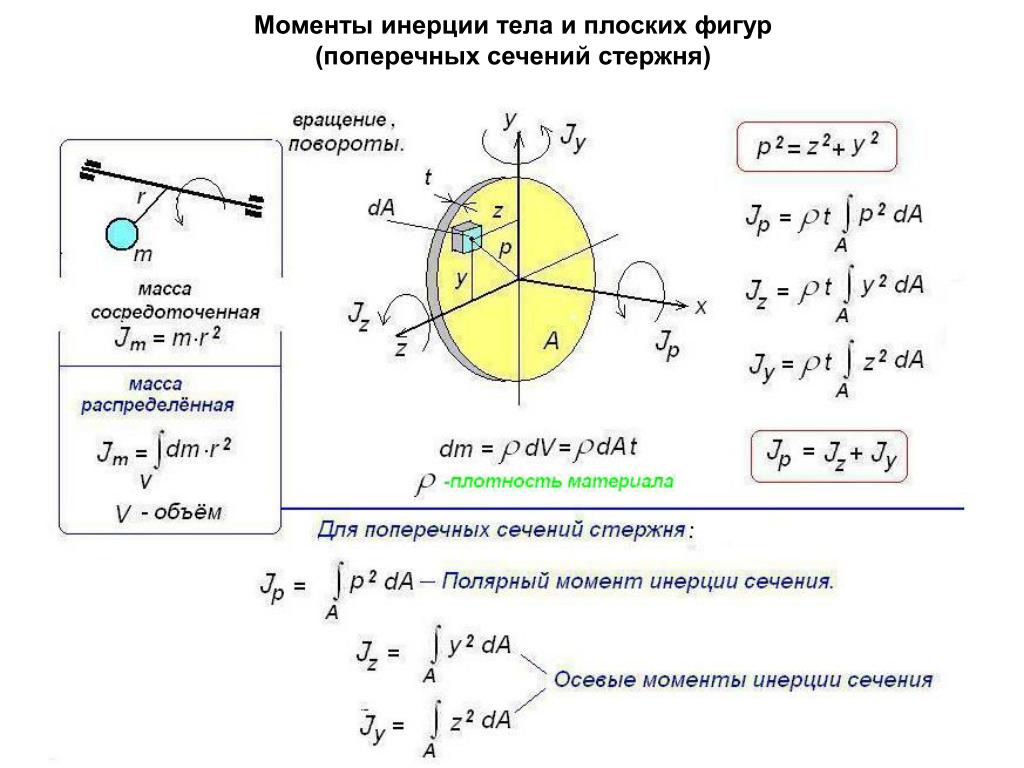
Очень важно отметить, что теорема о параллельных осях верна только для I c или I G — в этой формуле нельзя использовать момент инерции относительно другой точки. Также ясно, что добавленный член всегда будет положительным (площадь, масса и квадрат расстояния не могут быть отрицательными). Это напоминание о том, что момент инерции относительно центроида (момент площади) или центра тяжести (момент массы) является наименьшим моментом инерции для этого объекта — относительно любой другой оси момент инерции будет больше.
Расстояние (r) в теореме о параллельных осях представляет собой расстояние, на которое мы перемещаем ось, которую мы фиксируем в момент или намерение. Допустим, мы пытаемся найти моменты инерции прямоугольника выше относительно точки P. Начнем с поиска I xx , I yy и J zz относительно центра тяжести прямоугольника (C) в момент инерции табл. Затем мы добавили бы площадь, умноженную на квадрат расстояния, к каждому, чтобы найти скорректированные моменты инерции относительно P. Расстояние, на которое мы перемещаемся по оси x для I xx , равно вертикальному расстоянию r x , расстояние, на которое мы перемещаемся ось Y для I yy — это расстояние по горизонтали r y , а расстояние, на которое мы переместим ось z (которая указывает за пределы страницы) для J zz , — это диагональ r z .
Расстояние, на которое мы перемещаемся по оси x для I xx , равно вертикальному расстоянию r x , расстояние, на которое мы перемещаемся ось Y для I yy — это расстояние по горизонтали r y , а расстояние, на которое мы переместим ось z (которая указывает за пределы страницы) для J zz , — это диагональ r z .
Корректировка центра масс осуществляется по аналогичной логике, используя массу, умноженную на квадрат расстояния, где расстояние показывает, насколько далеко вы перемещаете ось вращения в трехмерном пространстве.
Использование метода составных частей для нахождения момента инерции
Чтобы найти момент инерции тела с помощью метода составных частей, вам нужно начать с разбиения площади или объема на простые формы. Убедитесь, что каждая отдельная форма доступна в таблице моментов инерции, и вы можете рассматривать отверстия или вырезы как отрицательную площадь или массу.
Начните с разбиения площади или объема на простые части и пронумеруйте их. Отверстия или вырезы будут считаться отрицательными областями или массами.
Отверстия или вырезы будут считаться отрицательными областями или массами.Далее вы создадите таблицу для отслеживания значений. Выделите строку для каждой части, которую вы пронумеровали ранее, и включите последнюю «итоговую» строку, которая будет использоваться для некоторых значений. Большая часть работы по методу составных частей заключается в заполнении этой таблицы. Столбцы будут немного отличаться в зависимости от того, что вы ищете, но обычно вам потребуется следующее.
Большая часть работы по методу составных частей будет вращаться вокруг заполнения таблицы, подобной этой. Эта таблица содержит строки и столбцы, необходимые для нахождения моментов инерции прямоугольной площади (I xx и I yy ) для этого составного тела.- Площадь или масса каждой детали (площадь для моментов инерции площади или масса для моментов инерции масс). Помните, что вырезы должны быть перечислены как отрицательные области или массы.
- Центроид или положение центра масс (координаты X, Y и, возможно, Z).
 Большую часть времени мы будем находить момент инерции относительно центроида составной формы, и если он не указан вам явно, вам нужно будет найти его, прежде чем идти дальше. Подробнее об этом см. На странице «Центроиды и центр масс с помощью метода составных частей».
Большую часть времени мы будем находить момент инерции относительно центроида составной формы, и если он не указан вам явно, вам нужно будет найти его, прежде чем идти дальше. Подробнее об этом см. На странице «Центроиды и центр масс с помощью метода составных частей». - Значения момента инерции относительно центроида каждой фигуры. Чтобы найти эти значения, вы подставите значения высоты, радиуса, массы и т. д. в формулы таблицы моментов инерции. Не используйте эти формулы вслепую, так как вам может понадобиться мысленно повернуть тело и, таким образом, поменять местами уравнения, если ориентация фигуры в таблице не совпадает с ориентацией фигуры на вашей диаграмме.
- Регулировочные расстояния (r) для каждой формы. Для этого значения вы захотите определить, как далеко перемещается ось x, ось y или z, чтобы пройти от центра тяжести детали до общего центра тяжести или точки, относительно которой вы берете момент инерции. Чтобы рассчитать эти значения в целом, вам нужно будет найти расстояния по горизонтали, вертикали или диагонали между центроидами частей и общими центроидами, которые вы указали ранее в таблице.
 См. раздел теоремы о параллельных осях на этой странице ранее для более подробной информации.
См. раздел теоремы о параллельных осях на этой странице ранее для более подробной информации. - Наконец, у вас будет столбец скорректированных моментов инерции. Возьмите первоначальный момент инерции относительно центроида, а затем просто добавьте площадь, умноженную на r в квадрате, или массу, умноженную на r в квадрате, для этого скорректированного значения.
Общий момент инерции вашего составного тела — это просто сумма всех скорректированных моментов инерции частей, которая будет суммой значений в последнем столбце (или столбцах, если вы находите моменты инерции относительно более чем одной оси).
Инерция вращения: определение и формула
Вы когда-нибудь крутились на офисном стуле? Да ладно, мы все это сделали. Есть что-то в стуле на колесах, что пробуждает в нас самого сокровенного ребенка. Теперь мы оба знаем, что даже малейший вкус скорости только заставляет нас хотеть двигаться быстрее, и поэтому, пробуя воду движения стула, вы, вероятно, экспериментировали со способами того, как вращаться быстрее. Это, вероятно, включало в себя прижатие рук и ног к себе. Вращательная инерция — это правильный физический термин, объясняющий, почему вы быстрее вращаетесь на офисном стуле, когда ваши руки и ноги подвернуты, а не расставлены.
Это, вероятно, включало в себя прижатие рук и ног к себе. Вращательная инерция — это правильный физический термин, объясняющий, почему вы быстрее вращаетесь на офисном стуле, когда ваши руки и ноги подвернуты, а не расставлены.
Рис. 1. Ускорение вращения на офисных стульях за счет поджимания рук и ног напрямую связано с принципом инерции вращения.
Так что да, есть фундаментальная причина, почему вы вращаетесь быстрее, как мяч, чем как тряпичная кукла. В этой статье мы рассмотрим эту фундаментальную причину и сосредоточимся в основном на инерции вращения — ее определении, формуле и применении — а затем завершим ее несколькими примерами.
Определение инерции вращения
Начнем с определения инерции.
Инерция — сопротивление объекта движению.
Мы обычно измеряем инерцию массой, что имеет смысл; у вас уже есть концептуальное понимание инерции, потому что вы знаете, что более тяжелые предметы труднее сдвинуть. Например, валун оказывает большее сопротивление движению, чем лист бумаги. Но что произойдет, если объект не движется по линии, а вращается? Тогда нам нужно говорить о r вращательной инерции.
Но что произойдет, если объект не движется по линии, а вращается? Тогда нам нужно говорить о r вращательной инерции.
Вращательная инерция — сопротивление объекта вращательному движению.
Масса — это то, как мы в некотором смысле «измеряем» инерцию. Но опыт говорит нам, что крутиться на стуле может быть легче или сложнее в зависимости от того, как мы позиционируем себя на стуле. Следовательно, инерция вращения связана с массой и распределением этой массы относительно оси вращения.
Кроме того, несмотря на то, что мы ссылались на объект выше, лучшим термином будет жесткая система .
Жесткая система — это объект или совокупность объектов, которые могут испытывать воздействие внешней силы и сохранять свою форму.
Например, вы можете толкнуть кусок желе, и он останется соединенным, но в некоторых местах он может быть согнут; это не жесткая система. В то время как кто-то мог бы подтолкнуть импровизированную модель солнечной системы 3-го класса к такой планете, как Юпитер, и все, что она будет делать, это вращаться: ее форма останется неизменной, все планеты по-прежнему будут выстраиваться вокруг Солнца, и она будет вращаться только немного.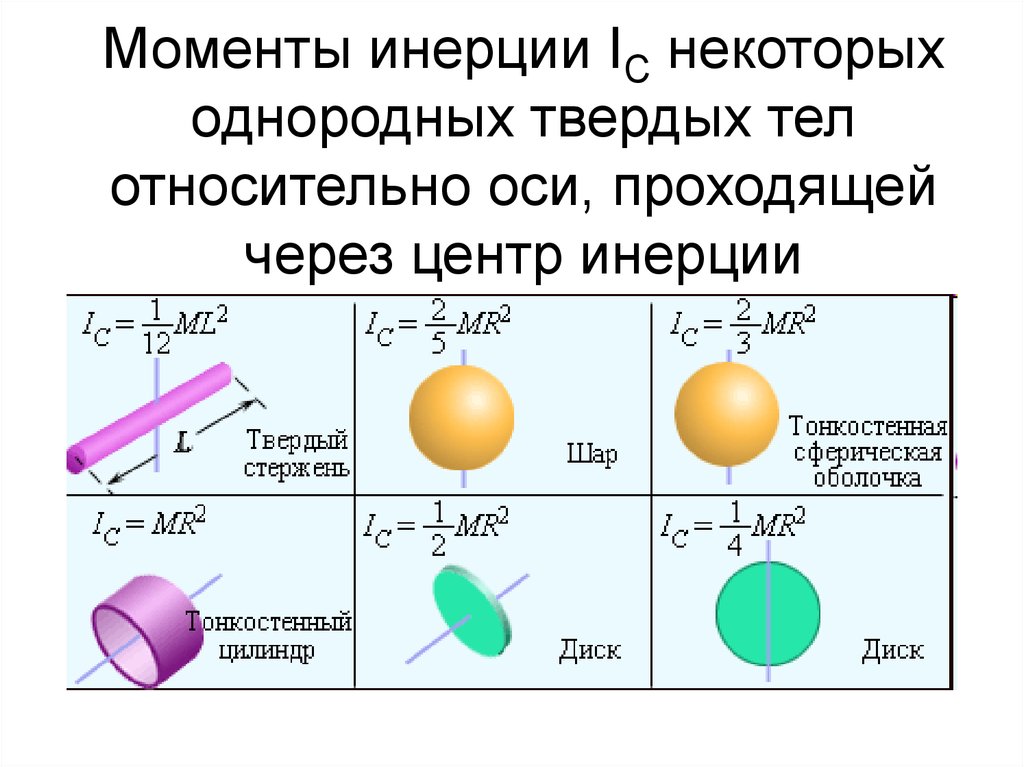 92$$
92$$
где \(I\) — инерция вращения, \(m\) — масса, а \(r\) — расстояние от оси, к которой перпендикулярно вращается объект.
Рис. 2. На этом изображении показан вид сверху и вертикальный вид параметров формулы инерции вращения. Обратите внимание, что \(r\) — это расстояние от оси вращения.
Суммарная инерция вращения
Полная инерция вращения твердой системы находится путем сложения всех индивидуальных инерций вращения частиц, образующих систему; математическое выражение 92 \mathrm{d}m$$
— это уравнение, которое мы можем использовать, используя \(\mathrm{d}m\) как каждый маленький бит массы и \(r\) как перпендикулярное расстояние от каждого \(\ mathrm{d}m\) к оси, вокруг которой вращается твердое тело.
Вращательная инерция и жесткие системы
По мере приближения массы к оси вращения наш радиус \(r\) уменьшается, резко уменьшая инерцию вращения, потому что \(r\) в нашей формуле возводится в квадрат. Это означает, что обруч с той же массой и размером, что и цилиндр, будет иметь большую инерцию вращения, потому что большая часть его массы расположена дальше от оси вращения или центра масс.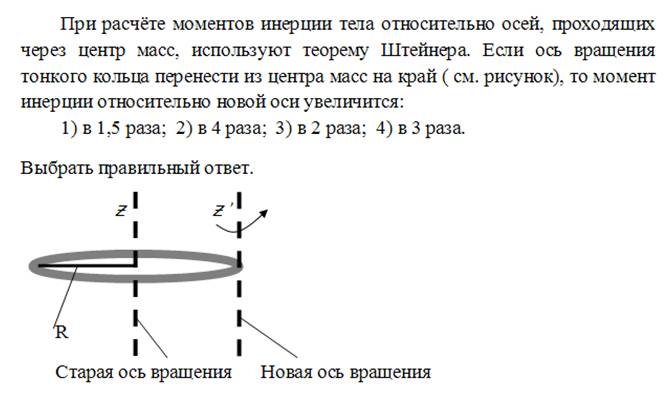
Одна из ключевых концепций, которые вам необходимо усвоить об инерции вращения, заключается в том, что инерция вращения жесткой системы в заданной плоскости минимальна, когда ось вращения проходит через центр масс системы. И если мы знаем момент инерции относительно оси, проходящей через центр масс, мы можем найти момент инерции относительно любой другой оси, параллельной ей, используя следующий результат.
Теорема о параллельных осях утверждает, что если мы знаем инерцию вращения системы относительно оси, проходящей через ее центр масс, \( I_\text{cm}, \), то мы можем найти инерцию вращения системы , \(I’\) относительно любой оси, параллельной ей, как сумма \(I_\text{cm}\) и произведения массы системы, \(m,\) умноженной на расстояние от центра масс, \(г\). 92.$$
Если вы хотите узнать, почему здесь есть \(\frac{1}{2}\\\), ознакомьтесь с разделом «Приложения вращательной инерции».
Какова инерция вращения диска \(3,0\,\mathrm{кг}\) с радиусом \(4,0\,\mathrm{м}\)?
В этом случае радиус диска равен расстоянию от оси, где происходит перпендикулярное вращение.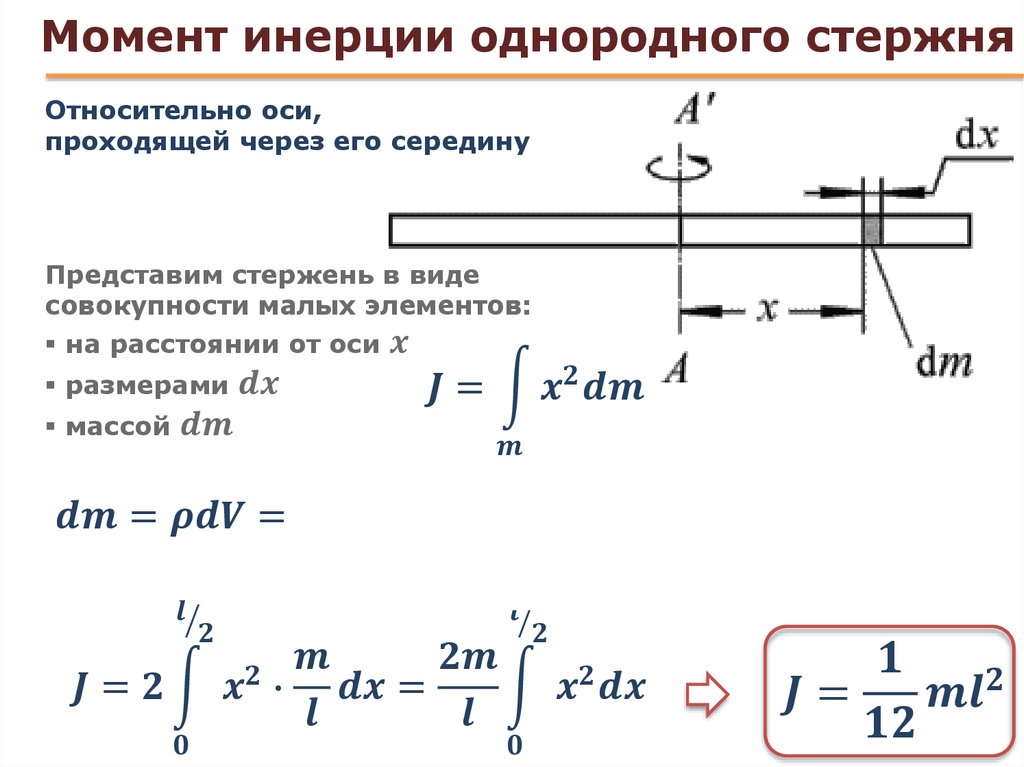 2, $ $ 92 \mathrm{d}m\mathrm{,}$$
2, $ $ 92 \mathrm{d}m\mathrm{,}$$
, который описывает инерцию вращения твердого тела, состоящего из множества различных крошечных элементов массы \(\mathrm{d}m\).
Если рассматривать наш диск как множество различных бесконечно тонких колец, мы можем сложить инерцию вращения всех этих колец, чтобы получить общую инерцию вращения диска. Напомним, что мы можем складывать бесконечно малые элементы, используя интегралы.
Рис. 5. Это пример диска с кольцом в поперечном сечении, которое мы могли бы использовать для интегрирования с окружностью/длиной \(2\pi r\) и шириной \(\mathrm{d} р\). 92\mathrm{.}$$
Приведенный выше вывод показывает полезность инерции вращения и ее различных формул. Теперь вы готовы покорить мир! Теперь вы готовы заняться вращательной инерцией и такими вещами, как крутящий момент и угловое движение. Если вы когда-нибудь будете участвовать в соревнованиях по вращению офисного стула, вы знаете, как победить, вам просто нужно переместить свой вес ближе к оси вращения, так что подтяните руки и ноги!
Вращательная инерция – ключевые выводы
- Вращательная инерция 92.



 Н. Курс теоретической механики. М.: МГУ, 1974. — 647 с.
Н. Курс теоретической механики. М.: МГУ, 1974. — 647 с.
 Большую часть времени мы будем находить момент инерции относительно центроида составной формы, и если он не указан вам явно, вам нужно будет найти его, прежде чем идти дальше. Подробнее об этом см. На странице «Центроиды и центр масс с помощью метода составных частей».
Большую часть времени мы будем находить момент инерции относительно центроида составной формы, и если он не указан вам явно, вам нужно будет найти его, прежде чем идти дальше. Подробнее об этом см. На странице «Центроиды и центр масс с помощью метода составных частей».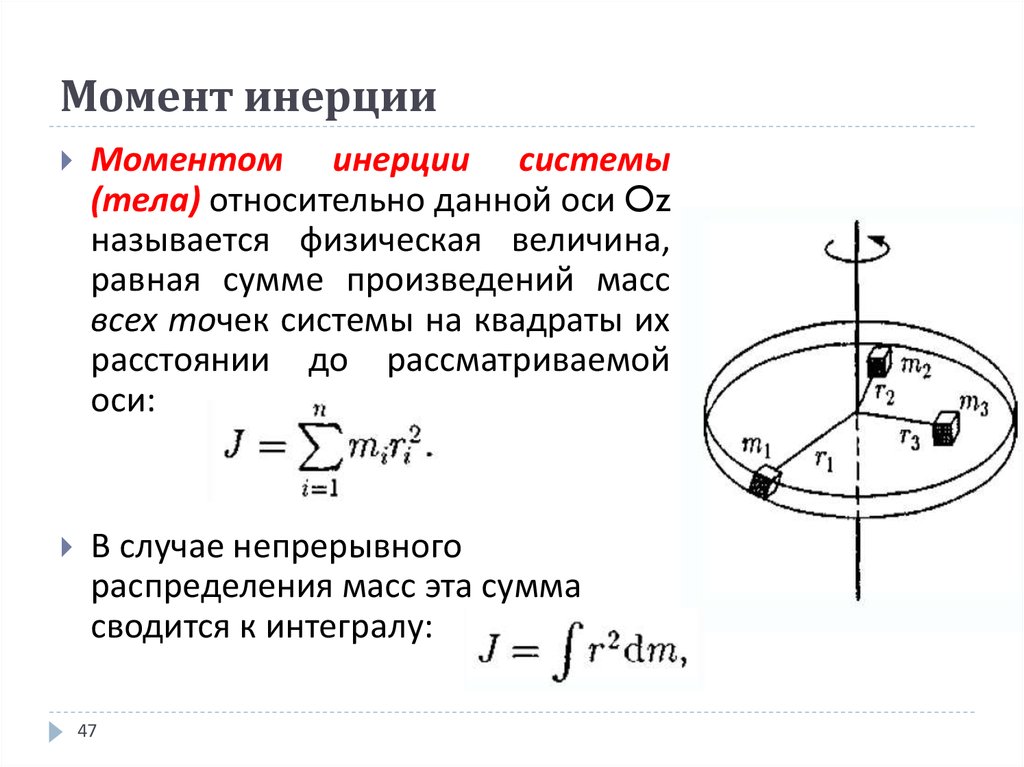 См. раздел теоремы о параллельных осях на этой странице ранее для более подробной информации.
См. раздел теоремы о параллельных осях на этой странице ранее для более подробной информации.