Потенциал электрического поля
Циркуляция и ротор(математическое отступление).
Как мы видели в пункте 1,
работа электростатического поля оказалась равной криволинейному интегралу, вычисленному
вдоль траектории, по которой движется заряд.
Вообще в математике криволинейный интеграл от любой векторной функции
по кривой (контуру) L означает следующее.
Разделим всю кривую на очень малые элементы
и получим векторы с направлениями,
определяемыми выбором движения, модули которых равны длинам этих участков; для
каждого вычислим скалярное произведение ;
просуммируем
полученные результаты; переходя к пределу бесконечно малых элементов кривой,
получим криволинейный интеграл (или интеграл по контуру).
Пусть теперь в области пространства, в которой определено векторное поле расположена
произвольная замкнутая кривая L (рис.6.3).
| def: Циркуляцией вектора по произвольному замкнутому контуру L называется криволинейный интеграл Г , (6.  7) 7)где — единичный вектор, касательный к контуру L, указывающий направление обхода этого контура. |
Фактически интегрируется только касательная составляющая
векторного поля Аl, поэтому помимо (6.7) для обозначения циркуляции
используют ещё следующие эквивалентные формулы:
.
Будем, кроме того, считать, что на контуре выбрано положительное
направление обхода, то есть направление, при движении, вдоль которого область,
ограниченная контуром, остаётся всегда слева (более точно см. ниже).
Вновь вспомним о гидродинамике. Если мы рассмотрим векторное
поле скоростей текущей
жидкости, и поместим в произвольную точку этой жидкости небольшую турбинку (колёсико
с лопастями) то в зависимости от своей ориентации, турбинка будет вращаться
с большей или меньшей скоростью. Если вычислить циркуляцию вектора скорости
вдоль контура, совпадающего с ободом турбинки, а затем разделить на длину этого
обода, то мы получим (в соответствие с теоремой о среднем) некоторое среднее
значение проекции скорости частиц жидкости на касательную к контуру vl. Но именно
Но именно
с такой линейной скоростью и будут вращаться лопасти турбинки. Таким образом,
чем больше циркуляция вектора скорости, тем с большей скоростью будет вращаться
турбинка, помещённая в данную точку жидкости, а это в свою очередь означает,
большую завихрённость жидкости в рассматриваемой точке. (Характерный пример
— вода, вытекающая из ванны.)
Следует отметить, однако, что характеризовать
завихрённость поля непосредственно циркуляцией Г нельзя, поскольку поле может
быть очень неоднородным, и степень его завихрённости будет изменяться от точки
к точке. Желая же определить такую «локальную» завихрённость, мы должны будем
уменьшать размеры контура L, стягивая его в точку. При этом,
очевидно, циркуляция будет стремиться к 0. В связи с этим, для характеристики
степени завихрённости поля вводят понятие плотности циркуляции, определяя её
как предел, к которому стремится отношение циркуляции вектора
по контуру L, к площади
DS,
ограниченной этим контуром, когда данный контур стягивается
к рассматриваемой точке пространства. (При этом, соответственно, DS0):
(При этом, соответственно, DS0):
.
Вычисляя этот предел, мы будем иметь уже некоторое конечное,
отличное от нуля число. Однако, это значение будет зависеть от ориентации контура L в поле.
Например, как уже говорилось ранее,
от ориентации турбинки в жидкости. Изменяя ориентацию турбинки, мы можем получить
максимальное и минимальное значения Г (соответствующие двум противоположным
ориентациям турбинки, при этом одно из них будет положительным, а другое отрицательным),
а также при некоторой ориентации турбинка вообще перестанет вращаться, что соответствует
Г=0. Данные обстоятельства показывают, что всё многообразие значений плотности
циркуляции векторного поля может быть, вообще говоря, представлено в виде проекции
некоторого вектора, на нормаль к площадке контура L. При этом данный вектор
по абсолютной величине будет равен максимальному значению плотности циркуляции
вектора в рассматриваемой
точке пространства, и направлен в сторону, соответствующую направлению нормали
к контуру L, при которой плотность циркуляции принимает это максимальное значение.
Данный вектор называется ротором или вихрем векторного поля
(от французского
(или английского) слова rotation — вращение, или лат. roto- вращаюсь) и проекция этого
вектора на любое направление в каждой точке пространства определяется
выражением:
(6.10)
Здесь — нормаль
к площадке DS, согласованная с направлением обхода контура L
правилом правого винта (буравчика) — рис.6.4.
Физика для средней школы
Разность потенциалов. Напряжение
Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2 поля
Выразим потенциальную энергию через потенциалы поля в соответствующих точках:
Тогда
Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.
Из этой формулы разность потенциалов
Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.
В СИ единицей разности потенциалов является вольт (В).
1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.
Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов часто называют электрическим напряжением между данными точками поля:
Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.
Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.
1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж.
1 МэВ = 106 эВ = 1,6·10-13 Дж.
Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.
Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.
Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле
Значит,
Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.
Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 1.
Рис. 1
Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 1, а).
Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. {2}}}\right).}
{2}}}\right).}
Относительное замедление хода времени в точке с меньшим значением гравитационного потенциала по сравнению с временем в точке с большим значением гравитационного потенциала равно разности гравитационных потенциалов в этих точках, делённой на квадрат скорости света.
Дивергенция и ротор (Как вы это поняли).
На рис.6.7 представлены различные картины векторного поля. Попробуйте сказать,
где ротор и дивергенция равны 0, а где нет
При этом прежде всего нужно обратить
внимание на контуры интегрирования, заметив, что они выбраны так, чтобы вдоль
каждой из сторон, проекция векторов поля имела одно и тоже значение (причём
для двух сторон в случаях а, б, г, д она равна 0)
Ответ:
| a) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. ротор не равен нулю. Сравните с рекой. | б) Явно виден источник поля. Дивергенция не равна нулю. Поле центрально — симметричное.  Поэтому ротор равен 0. Поэтому ротор равен 0. | в) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Проекции векторов поля на противоположные стороны контура разных знаков, но одинаковы по абсолютной величине, и поэтому при сложении линейных интегралов они уничтожают друг друга. Поэтому ротор равен нулю. |
| г) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор убывает по мере удаления от центра поля (за пределами рисунка) поэтому ротор может быть равен 0. | д) вектор постоянен вдоль своего направления, следовательно, дивергенция равна 0. Вектор не убывает, поэтому линейный интеграл по левой стороне контура не компенсируется таким же интегралом по правой. Поэтому ротор не равен нулю. | е) Явно виден сток поля. Поэтому дивергенция не равна 0. Так же и ротор не равен нулю, поскольку циркуляция вдоль указанного контура не равна 0, так как проекции векторов поля на все стороны контура одного знака (отрицательны) и при сложении (интегрировании) не компенсируют друг друга.  |
Подводя итог, ещё раз отметим, что ротор характеризует степень
завихрённости векторного поля, его «вращательную составляющую». При этом, однако,
нужно иметь в виду, что данная «вращательная компонента» поля может быть обусловлена
не только искривлением векторных линий (завихрённость «в чистом виде»), как
при вытекании воды из ванны, или в примере е), но и поперечной неоднородностью
поля, когда векторные линии — прямые, как в случае течения воды в реке (рис.6.5),
или в случае примера а).
Химическая работа
Для однородных многокомпонентных систем открытых систем
- dE=TdS−PdV+∑jμjdmj,{\displaystyle dE=TdS-PdV+\sum _{j}\mu _{j}dm_{j},}
где mj{\displaystyle m_{j}} — масса j{\displaystyle j}-го компонента, μj{\displaystyle \mu _{j}} — химический потенциал этого компонента, по определению равный
μk≡(∂E∂mk)S,V,{mj≠k}.{\displaystyle \mu _{k}\equiv \left({\frac {\partial E}{\partial m_{k}}}\right)_{S,V,\{m_{j\neq k}\}}.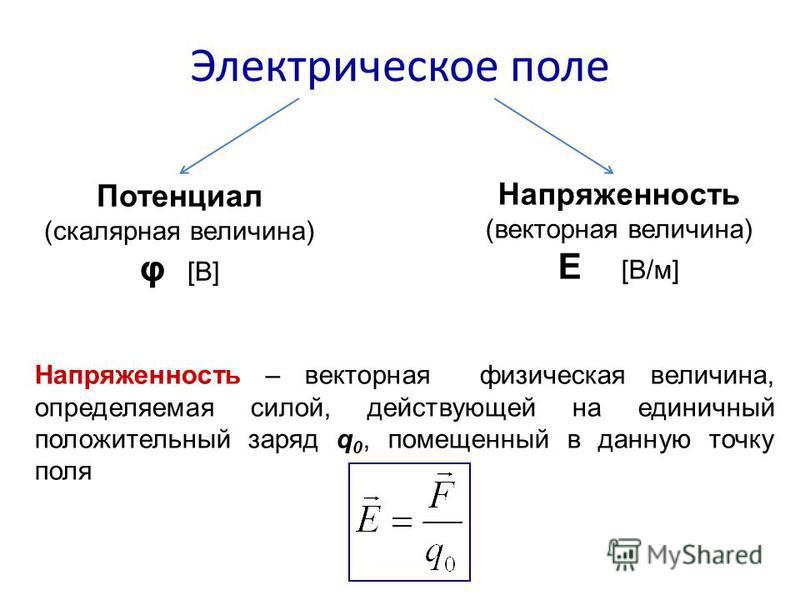 } } | (Дефиниция химического потенциала компонента) |
Величину изменение энергии системы за счёт вариации масс составляющих систему веществ
| z≡∑jμjdmj,{\displaystyle z\equiv \sum _{j}\mu _{j}dm_{j},} | (Химическая работа бесконечно малого процесса в открытой однородной системе) |
не имеющую общепринятого названия, чаще всего называют элементарной химической работой, а также массовой работой, работой переноса массы, работой перераспределения масс веществ, энергией, передаваемой при обмене веществом, энергией, передаваемой при переносе массы. Химическая работа не является независимо измеряемой величиной — таковой является сумма энтропийной и химической составляющих изменения энергии в рассматриваемом процессе. Но если положить теплоту бесконечно малого процесса равной
| q≡TdS{\displaystyle q\equiv T\mathrm {d} S} | (Теплота бесконечно малого процесса в открытой однородной системе) |
и учесть, что элементарная работа расширения/сжатия равна
| w=−PdV,{\displaystyle w=-P\mathrm {d} V,} | (Элементарная работа расширения/сжатия в однородной системе) |
то химическая работа может быть вычислена:
- z=∑jμjdmj=dE−q−w=dE−TdS+PdV.
 {\displaystyle z=\sum _{j}\mu _{j}\mathrm {d} m_{j}=\mathrm {d} E-q-w=\mathrm {d} E-T\mathrm {d} S+P\mathrm {d} V.}
{\displaystyle z=\sum _{j}\mu _{j}\mathrm {d} m_{j}=\mathrm {d} E-q-w=\mathrm {d} E-T\mathrm {d} S+P\mathrm {d} V.}
Похожие слова
ПотенцияПотенциацияПотенциальноПотенциометрПотенциальныйПотенцироватьПотенциометрияПотенциалоскопПотенцированиеПотенциал покояПотенцированныйПотенциальностьПотенциал теченияПотенциальная ямаПотенциал действияПотенциальные силыПотенциал осажденияПотенциал ионизацииПотенциал зажиганияПотенциальный барьерПотенциал поврежденияПотенциальная энергияПотенциалы запаздывающиеПотенциал концевой пластинкиПотенциалы термодинамическиеПотенциал электростатическийПотенциация посттетаническаяПотенциалы электромагнитного поляПотенциал концевой пластинки миниатюрный
Что такое электрический потенциал простыми словами – Все об электричестве
Всем привет, на связи с вами снова Владимир Васильев. Новогодние празднования подходят к концу, а значить надо готовиться к рабочим будням, с чем вас дорогие друзья и поздравляю! Хех, только не надо расстраиваться и впадать в депрессию, нужно мыслить позитивно.
Так вот в эти новогодние праздники я как-то размышлял о аудитории моего блога: «Кто он? Кто тот посетитель моего блога, что каждый день заходит почитать мои посты?». Может быть это прошаренный спец зашел из любопытства почитать что я тут накалякал? А может это какой -нибудь доктор радиотехнических наук зашел посмотреть как спаять схему мультивибратора?
Электрический потенциал
Электрический потенциал – это скалярная физическая величина, характеризующая напряжённость поля. Через параметр также выражается электрическое напряжение.
Внешняя контактная разность — потенциал
В чем состоит разница в экспериментальном осуществлении внешней и внутренней контактной разности потенциалов. В чем состоят физические механизмы возникновения внутренней и внешней контактной разности потенциалов.
| Диаграмма потенциальной энергии электрона в случае контакта двух. |
Произведение заряда электрона е на) представляет собой работу выхода электрона из металла. Разность т я — г 2 ек называется внешней контактной разностью потенциалов.
Разность т я — г 2 ек называется внешней контактной разностью потенциалов.
Сопоставляя это выражение с уравнением ( VIII, 22), мы видим, что Е ек. Следовательно, разность между потенциалами точек нулевых зарядов двух металлов численно равна внешней контактной разности потенциалов между ними. Этот вывод, сделанный А. Н. Фрумкиным, заставляет рассматривать ф ( 0) как весьма важную физическую характеристику металлов.
Это произошло потому, что мы не учли энергию UK, обусловленную внешней контактной разностью потенциалов Фк, которую необходимо добавить к общей энергии или отнять от нее в зависимости от направления обхода.
Сопоставляя это выражение с уравнением ( VIII, 22), мы видим, что Е — ек. Следовательно, разность между потенциалами то ек нулевых зарядов двух металлов численно равна внешней контактной разности потенциалов между ними. Этот вывод, сделанный А. Н. Фрумкиным, заставляет рассматривать q ( 0) как весьма важную физическую характеристику металлов.
Поверхность калия в фотоэлементе освещают светом длиной волны 95 ммк. Определить минимальную величину задерживающей разности потенциалов, которую необходимо приложить извне для полного прекращения фототока, если известно, что внешняя контактная разность потенциала, равная 0 7 в, направлена противоположно приложенному напряжению.
В случае контакта двух разнородных металлов при выходе электрона из одного металла в другой совершается работа, равная разности работ выхода соприкасающихся металлов. Значения контактных потенциалов выхода зависят от рода металлов, а также от состояния соприкасающихся поверхностей и находятся в пределах от нескольких десятых долей вольта до нескольких вольт. Таким образом, внешняя контактная разность потенциалов значительно превосходит внутреннюю.
| Контур из двух разнородных металлов в растворе электролита. |
Оба вывода электрометра находятся в одной и той же фазе — вакууме. Как показывает опыт, стрелка электрометра отклоняется при такой установке, подтверждая наличие разности потенциалов между двумя точками в вакууме, находящимися на близком расстоянии от поверхности двух различных металлов, контактирующих между собой. Эта разность потенциалов носит название внешней контактной разности потенциалов или, иначе, вольта-потенциала. Обозначим ее величину символом AV.
Как показывает опыт, стрелка электрометра отклоняется при такой установке, подтверждая наличие разности потенциалов между двумя точками в вакууме, находящимися на близком расстоянии от поверхности двух различных металлов, контактирующих между собой. Эта разность потенциалов носит название внешней контактной разности потенциалов или, иначе, вольта-потенциала. Обозначим ее величину символом AV.
Фотоэлемент состоит из двух разнородных электродов, один из которых освещают монохроматическим светом длиной волны 185 ммк. Фототек возникает лишь при наличии приложенного извне ускоряющего напряжения 0 4 в. Известно, кроме того, что внешняя контактная разность потенциалов между данными электродами равна 1 81 в.
В этом случае перераспределение ионов между электродом и раствором не будет и двойной электрический слой не возникает. Такой раствор называется нулевым раствором, а электрический потенциал на электроде — потенциалом нулевого заряда. Разность потенциалов двух электродов в нулевом растворе равна внешней контактной разности потенциалов электродов, которая, в свою очередь, определяется разностью работ выхода электронов для этих металлов. Так, при контакте двух разных металлов электроны с поверхности одно-то из них переходят на поверхность другого до установления равновесия и постоянной разности потенциалов, равной разности между их потенциалами пулевых зарядов.
Разность потенциалов двух электродов в нулевом растворе равна внешней контактной разности потенциалов электродов, которая, в свою очередь, определяется разностью работ выхода электронов для этих металлов. Так, при контакте двух разных металлов электроны с поверхности одно-то из них переходят на поверхность другого до установления равновесия и постоянной разности потенциалов, равной разности между их потенциалами пулевых зарядов.
| При соприкосновении двух различных металлов во внешнем пространстве появляется электрическое поле, а на поверхности металлов возникают заряды. |
Согласно сказанному выше на обоих проводниках появляются электрические заряды, а между свободными их концами возникает электрическое поле. Разность потенциалов между любыми двумя точками а ж б ( рис. 336), находящимися вне проводников, но расположенными в непосредственной близости от их поверхностей, называется внешней контактной разностью потенциалов или просто контактной разностью потенциалов.
Правая часть последнего равенства представляет собой внешнюю контактную разность потенциалов обоих металлов Мех и Ме. Если теперь электрон из точки а возле поверхности металла Мех перенести в точку Ь в вакууме, то работа переноса по этому второму пути будет равна произведению заряда электрона на внешнюю контактную разность потенциалов для металлов Мех и Me, — так называемый вольта-потенциал, который ранее мы обозначали символом ДУ.
Гравитационный потенциал точечной массы и произвольного тела
Гравитационный потенциал, создаваемый точечной массой M{\displaystyle M}, расположенной в начале координат, равен
- φ(r→)=−GMr+C,{\displaystyle \varphi ({\vec {r}})=-{\frac {GM}{r}}+C,}
где G{\displaystyle G} — гравитационная постоянная, r{\displaystyle r} — расстояние от начала координат (модуль радиус-вектора r→{\displaystyle {\vec {r}}}). Через C{\displaystyle C} обозначена произвольная константа, опускаемая при выборе φ={\displaystyle \varphi =0} на бесконечности. {\prime })}; интегрирование выполняется по всему объёму тел, создающих поле.
{\prime })}; интегрирование выполняется по всему объёму тел, создающих поле.
В электродинамике
Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция ∫CE⋅dℓ{\displaystyle \textstyle \int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}} зависит от пути, потому что ∇×E≠{\displaystyle \mathbf {\nabla } \times \mathbf {E} \neq \mathbf {0} } (см. Закон индукции Фарадея).
Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности, А определен так чтобы
- B=∇×A,{\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} ,\,}
где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. {b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)},\,}
{b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)},\,}
в отличие от электростатики.
Литература
- (недоступная ссылка)
- Химический потенциал // : / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- Большая физическая энциклопедия в 5-ти томах. Гл. ред. А. М. Прохоров. Москва «Советская энциклопедия» 1988 г.
- (недоступная ссылка)
- (недоступная ссылка)
- (недоступная ссылка)
- (недоступная ссылка)
- Гуггенгейм. Современная термодинамика, изложенная по методу У. Гиббса / Пер. под ред. проф. С. А. Щукарева. — Л.—М.: Госхимиздат, 1941. — 188 с.
- (недоступная ссылка)
- Заславский Б. В. Краткий курс сопротивления материалов. — М.: Машиностроение, 1986. — 328 с.
- Зимон А. Д. Коллоидная химия: Общий курс. — 6-е изд. — М.: Красанд, 2015. — 342 с. — ISBN 978-5-396-00641-6.
- (недоступная ссылка)
- (недоступная ссылка)
- (недоступная ссылка)
- Мейз Дж.
 Теория и задачи механики сплошных сред. — М.: Мир, 1974. — 319 с.
Теория и задачи механики сплошных сред. — М.: Мир, 1974. — 319 с. - (недоступная ссылка)
- (недоступная ссылка)
- Румер Ю. Б., Рывкин М. Ш. Термодинамика, статистическая физика и кинетика. М., Наука, 1977. 552 с.
- Русанов А. И. Лекции по термодинамике поверхностей. — СПб.—М.—Краснодар: Лань, 2013. — 237 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1487-1.
- Салем Р. Р. Физическая химия. Термодинамика. — М.: Физматлит, 2004. — 351 с. — ISBN 5-9221-0078-5.
- (недоступная ссылка)
- Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
- Тер Хаар Д., Вергеланд Г. Основы термодинамики / Пер. с англ.. — М.: Вузовская книга, 2006. — 200 с. — ISBN 5-9502-0197-3.

- Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5: Стробоскопические приборы — Яркость. — 760 с. — ISBN 5-85270-101-7.
- (недоступная ссылка)
- Guggenheim E. A. Thermodynamics: An Advanced Treatment for Chemists and Physicists. — Amsterdam: North-Holland, 1985. — xxiv + 390 с. — ISBN 0 444 86951 4.
Физика для средней школы
Потенциал
Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система «заряд — электростатическое поле» обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:
Если Wp2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда q равна работе, которая была бы совершена при перемещении заряда q из данной точки в точку с нулевой энергией.
Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q (рис. 1).
Рис. 1
Будем помещать в точку М этого поля различные пробные положительные заряды q. Потенциальная энергия их различна, но отношение для данной точки поля и служит характеристикой поля, называемой потенциалом поля в данной точке:
Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).
Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд, помещенный в эту точку, к значению заряда.
Потенциал — это энергетическая характеристика поля в отличие от напряженности поля, являющейся силовой характеристикой поля.
Необходимо отметить, что потенциальная энергия заряда в данной точке поля, а значит, и потенциал зависят от выбора нулевой точки. Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.
Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.
Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал можно определить только с точностью до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.
В технике принято считать нулевой точкой любую заземленную точку, т.е. соединенную проводником с землей. В физике за начало отсчета потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если нулевая точка выбрана, то потенциальная энергия (соответственно и потенциал в данной точке) заряда q становится определенной величиной.
На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой
При указанном выше выборе нулевой точки потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:
По этой формуле можно рассчитывать потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R в точках, находящихся на поверхности сферы и вне ее. Внутри сферы потенциал такой же, как и на поверхности, т.е.
Внутри сферы потенциал такой же, как и на поверхности, т.е.
Если электростатическое поле создается системой зарядов, то имеет место принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:
Зная потенциал поля в данной точке, можно рассчитать потенциальную энергию заряда q0 помещенного в эту точку: Wp1 = q. Если положить, что Wp2 = 0, то из уравнения (1) будем иметь
Потенциальная энергия заряда q в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q0 из данной точки в нулевую. Из последней формулы имеем
Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в нулевую (в бесконечность).
Потенциальная энергия заряда q помещенного в электростатическое поле точечного заряда q на расстоянии r от него,
Если q и q — одноименные заряды, то , если q и q — разные по знаку заряды, то .
Отметим еще раз, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение Wp выбрано ее значение при r = бесконечности.
Если электростатическое поле образовано системой n точечных электрических зарядов, то потенциальная энергия системы определяется по формуле
где — потенциал поля, созданного всеми зарядами, кроме заряда qi, в той точке поля, где находится заряд qi.
Нервные импульсы
Если мозг принимает решение выполнить действие, то отправляет команду в виде импульса, который отбивается от конца, где осуществляется мышечное сжатие.
Нейроны получают импульс у дендритов. Он перемещается сквозь аксон – длинное расширение клетки в виде электрического потенциала, который создается при разнообразных концентрациях натрия и калия по обе стороны мембраны.
Дендриты посылают нейронам импульсы. Они перемещаются сквозь аксон. Это вытянутая ячейка в виде электрического потенциала, формируемого разнообразными концентрациями ионов натрия и калия по обе стороны от мембраны
Когда сигнал доходит к концу аксона, то выходят наружу нейротрансмиттеры, которые перехватываются дендритами следующего нейрона (повторяет предыдущий процесс).
| Обзор |
|
| Эквипотенциальные поверхности и линии |
|
| Зарядка |
|
| Конденсаторы и диэлектрики |
|
| Приложение |
Дзета-потенциал.
 Двойной электрический слой.
Двойной электрический слой.В дисперсных системах на поверхности частиц (на границе раздела частица-дисперсионная среда) возникает двойной электрический слой (ДЭС). Двойной электрический слой представляет собой слой ионов, образующийся на поверхности частицы в результате адсорбции ионов из раствора или диссоциации поверхностных соединений. Поверхность частицы приобретает слой ионов определенного знака, равномерно распределенный по поверхности и создающий на ней поверхностный заряд. Эти ионы называют потенциалопределяющими (ПОИ). К поверхности частицы из жидкой среды притягиваются ионы противоположного знака, их называют противоионами (ПИ).
Таким образом, двойной электрический слой состоит из потенциалопределяющих ионов и слоя противоионов, расположенных в дисперсионной среде. Слой противоионов состоит из двух слоев:
- Адсорбционный слой (плотный слой), примыкающий непосредственно к межфазной поверхности.

- Диффузный слой, в котором находятся противоионы. Эти противоионы притягиваются к частице за счет электростатических сил. Толщина диффузного слоя зависит от свойств системы и может достигать больших значений.
При движении частицы двойной электрический слой разрывается. Место разрыва при перемещении твердой и жидкой фаз друг относительно друга называется плоскостью скольжения. Плоскость скольжения лежит на границе между диффузными и адсорбционными слоями, либо в диффузном слое вблизи этой границы. Потенциал на плоскости скольжения называют электрокинетическим или дзета-потенциалом (ζ-потенциал).
Другими словами, дзета-потенциал — это разность потенциалов дисперсионной среды и неподвижного слоя жидкости, окружающего частицу.
Теории двойного электрического слоя широко используются для интерпретации поверхностных явлений. Однако не существует прямых методов измерения потенциалов на границе адсорбционного слоя. Для количественного определения величины электрического заряда в двойном электрическом слое широко используется дзета-потенциал. Дзета-потенциал не равен адсорбционному потенциалу или поверхностному потенциалу в двойном электрическом слое. Тем не менее, дзета-потенциал часто является единственным доступным способом для оценки свойств двойного электрического слоя. Знание дзета-потенциала важно во многих областях производственной и исследовательской деятельности.
Однако не существует прямых методов измерения потенциалов на границе адсорбционного слоя. Для количественного определения величины электрического заряда в двойном электрическом слое широко используется дзета-потенциал. Дзета-потенциал не равен адсорбционному потенциалу или поверхностному потенциалу в двойном электрическом слое. Тем не менее, дзета-потенциал часто является единственным доступным способом для оценки свойств двойного электрического слоя. Знание дзета-потенциала важно во многих областях производственной и исследовательской деятельности.
Строение двойного электрического слоя
Образование двойного электрического слоя приводит к появлению электрического потенциала, который убывает с расстоянием, и его значение в разных точках соответствует:
- Поверхностному потенциалу φ
- Потенциалу адсорбционного слоя φδ
- Дзета-потенциалу ζ
Важность определения дзета-потенциала
Важность дзета-потенциала состоит в том, что его значение может быть связано с устойчивостью коллоидных дисперсий.
Для молекул и частиц, которые достаточно малы, высокий дзета-потенциал будет означать стабильность, т.е. раствор или дисперсия будет устойчивы по отношению к агрегации. Когда дзета-потенциал низкий, притяжение превышает отталкивание, и устойчивость дисперсии будет нарушаться. Так, коллоиды с высоким дзета-потенциалом являются электрически стабилизированными, в то время, как коллоиды с низким дзета-потенциалом склонны коагулировать или флокулировать.
Значение дзета-потенциала равное 30 мВ (положительное или отрицательное) можно рассматривать как характерное значение, для условного разделения низко-заряженных поверхностей и высоко-заряженных поверхностей. Чем больше электрокинетический потенциал, тем устойчивее коллоид.
Таблица устойчивости коллоидной системы для различных значений дзета-потенциала.
| Дзета-потенциал | Устойчивость коллоидной системы |
| От 0 до ± 30 мВ | Плохая устойчивость (возможна коагуляция или флокуляция) |
| Больше ± 30 мВ | Хорошая устойчивость |
2_1 Мембранный потенциал покоя кратко (доцент Сазонов В.
 Ф.)Введение
Ф.)ВведениеЗачем нам нужно знать, что такое потенциал покоя?
Что такое «животное электричество»? Откуда в организме берутся «биотоки»? Как живая клетка, находящаяся в водной среде, может превратиться в «электрическую батарейку»?
— На эти вопросы мы сможем ответить, если узнаем, как клетка за счёт перераспределения электрических зарядов создаёт себе электрический потенциал на мембране.
Как работает нервная система? С чего в ней всё начинается? Откуда в ней берётся электричество для нервных импульсов?
— На эти вопросы мы также сможем ответить, если узнаем, как нервная клетка создаёт себе электрический потенциал на мембране.
Итак, понимание того, как работает нервная система, начинается с того, что надо разобраться, как работает отдельная нервная клетка — нейрон.
А в основе работы нейрона с нервными импульсами лежит перераспределение электрических зарядов на его мембране и изменение величины электрических потенциалов. Но чтобы потенциал изменять, его нужно для начала иметь. Поэтому можно сказать, что нейрон, готовясь к cвоей нервной работе, создаёт на своей мембране электрический потенциал, как возможность для такой работы.
Но чтобы потенциал изменять, его нужно для начала иметь. Поэтому можно сказать, что нейрон, готовясь к cвоей нервной работе, создаёт на своей мембране электрический потенциал, как возможность для такой работы.
Таким образом, наш самый первый шаг к изучению работы нервной системы — это понять, каким образом перемещаются электрические заряды на нервных клетках к как за счёт этого на мембране появляется электрический потенцила. Этим мы и займёмся, и назовём этот процесс появления электрического потенциала у нейронов — формирование потенциала покоя.
ОпределениеВ норме, когда клетка готова к работе, у неё уже есть электрический заряд на поверхности мембраны. Он называется мембранный потенциал покоя.
Потенциал покоя — это разность электрических потенциалов между внутренней и наружной сторонами мембраны, когда клетка находится в состоянии физиологического покоя. Его средняя величина составляет -70 мВ (милливольт).
«Потенциал» — это возможность, он сродни понятию «потенция». Электрический потенциал мембраны — это её возможности по перемещению электрических зарядов, положительных или отрицательных. В роли зарядов выступают заряженные химические частицы — ионы натрия и калия, а также кальция и хлора. Из них только ионы хлора заряжены отрицательно (-), а остальные — положительно (+).
Таким образом, имея электрический потенциал, мембрана может перемещать в клетку или из клетки указанные выше заряженные ионы.
Важно понимать, что в нервной системе электрические заряды создаются не электронами, как в металлических проводах, а ионами — химическими частицами, имеющими электрический заряд. Электрический ток в организме и его клетках — это поток ионов, а не электронов, как в проводах. Обратите также внимание на то, что заряд мембраны измеряется изнутри клетки, а не снаружи.
Если говорить уж совсем примитивно просто, то получается, что снаружи вокруг клетки будут преобладать «плюсики», т. е. положительно заряженные ионы, а внутри — «минусики», т.е. отрицательно заряженные ионы. Можно сказать, что внутри клетка электроотрицательна. И теперь нам всего лишь надо объяснить, как это так получилось. Хотя, конечно, неприятно сознавать, что все наши клетки — отрицательные «персонажи». ((
е. положительно заряженные ионы, а внутри — «минусики», т.е. отрицательно заряженные ионы. Можно сказать, что внутри клетка электроотрицательна. И теперь нам всего лишь надо объяснить, как это так получилось. Хотя, конечно, неприятно сознавать, что все наши клетки — отрицательные «персонажи». ((
Сущность
Сущность потенциала покоя — это преобладание на внутренней стороне мембраны отрицательных электрических зарядов в виде анионов и недостаток положительных электрических зарядов в виде катионов, которые сосредотачиваются на её наружной стороне, а не на внутренней.
Внутри клетки — «отрицательность», а снаружи — «положительность».
Такое положение вещей достигается с помощью трёх явлений: (1) поведения мембраны , (2) поведения положительных ионов калия и натрия и (3) соотношения химической и электрической силы.
1. Поведение мембраны
В поведении мембраны для потенциала покоя важны три процесса:
1) Обмен внутренних ионов натрия на наружные ионы калия. Обменом занимаются специальные транспортные структуры мембраны: ионные насосы-обменники. Таким способом мембрана перенасыщает клетку калием, но обедняет натрием.
Обменом занимаются специальные транспортные структуры мембраны: ионные насосы-обменники. Таким способом мембрана перенасыщает клетку калием, но обедняет натрием.
2) Открытые калиевые ионные каналы. Через них калий может как заходить в клетку, так и выходить из неё. Он выходит в основном.
3) Закрытые натриевые ионные каналы. Из-за этого натрий, выведенный из клетки насосми-обменниками, не может вернуться в неё обратно. Натриевые каналы открываются только при особых условиях — и тогда потенциал покоя нарушается и смещается в сторону нуля (это называется деполяризацией мембраны, т.е. уменьшением полярности).
2. Поведение ионов калия и натрия
Ионы калия и натрия по-разному перемещаются через мембрану:
1) Через ионные насосы-обменники натрий насильно выводится из клетки, а калий затаскивается в клетку.
2) Через постоянно открытые калиевые каналы калий выходит из клетки, но может и возвращаться в неё обратно через них же.
3) Натрий «хочет» войти в клетку, но «не может», т.к. каналы для него закрыты.
3. Соотношение химической и электрической силы
По отношению к ионам калия между химической и электрической силой устанавливается равновесие на уровне — 70 мВ.
1) Химическая сила выталкивает калий из клетки, но стремится затянуть в неё натрий.
2) Электрическая сила стремится затянуть в клетку положительно заряженные ионы (как натрий, так и калий).
Формирование потенциала покояПопробую рассказать коротко, откуда берётся мембранный потенциал покоя в нервных клетках — нейронах. Ведь, как всем теперь известно, наши клетки только снаружи положительные, а внутри они весьма отрицательные, и в них существует избыток отрицательных частиц — анионов и недостаток положительных частиц — катионов.
И вот тут исследователя и студента поджидает одна из логических ловушек: внутренняя электроотрицательность клетки возникает не из-за появления лишних отрицательных частиц (анионов), а наоборот — из-за потери некоторого количества положительных частиц (катионов).
И поэтому сущность нашего рассказа будет заключаться не в том, что мы объясним, откуда берутся отрицательные частицы в клетке, а в том, что мы объясним, каким образом в нейронах получается дефицит положительно заряженных ионов — катионов.
Куда же деваются из клетки положительно заряженные частицы? Напомню, что это ионы натрия — Na+ и калия — K+.
Натрий-калиевый насос
А всё дело заключается в том, что в мембране нервной клетки постоянно работают насосы-обменники, образованные специальными белками, встроенными в мембрану. Что они делают? Они меняют «собственный» натрий клетки на наружный «чужой» калий. Из-за этого в клетке оказывается в конце концов недостаток натрия, который ушёл на обмен. И в то же время клетка переполняется ионами калия, который в неё натащили эти молекулярные насосы.
Чтобы легче было запомнить, образно можно сказать так: «Клетка любит калий!» (Хотя об истинной любви здесь не может идти и речи!) Поэтому она и затаскивает калий в себя, несмотря на то, что его и так полно. Поэтому она невыгодно обменивает его на натрий, отдавая 3 иона натрия за 2 иона калия. Поэтому она тратит на этот обмен энергию АТФ. И как тратит! До 70% всех энергозатрат нейрона может уходить на работу натрий-калиевых насосов. Вот что делает любовь, пусть даже не настоящая!
Поэтому она невыгодно обменивает его на натрий, отдавая 3 иона натрия за 2 иона калия. Поэтому она тратит на этот обмен энергию АТФ. И как тратит! До 70% всех энергозатрат нейрона может уходить на работу натрий-калиевых насосов. Вот что делает любовь, пусть даже не настоящая!
Кстати, интересно, что клетка не рождается с потенциалом покоя в готовом виде. Например, при дифференцировке и слиянии миобластов потенциал их мембраны изменяется от -10 до -70 mV, т.е. их мембрана становится более электроотрицательной, она поляризуется в процессе дифференцировки . А в экспериментах на мультипотентных мезенхимальных стромальных клетках (ММСК) костного мозга человека искусственная деполяризация ингибировала дифференцировку клеток (Fischer-Lougheed J., Liu J.H., Espinos E. et al. Human myoblast fusion requires expression of functional inward rectifier Kir2.1 channels. Journal of Cell Biology 2001; 153: 677-85; Liu J.H., Bijlenga P., Fischer-Lougheed J. et al. Role of an inward rectifier K+ current and of hyperpolarization in human myoblast fusion. Journal of Physiology 1998; 510: 467-76; Sundelacruz S., Levin M., Kaplan D.L. Membrane potential controls adipogenic and osteogenic differentiation of mesenchymal stem cells. Plos One 2008; 3).
Journal of Physiology 1998; 510: 467-76; Sundelacruz S., Levin M., Kaplan D.L. Membrane potential controls adipogenic and osteogenic differentiation of mesenchymal stem cells. Plos One 2008; 3).
Образно говоря, можно выразиться так:
Создавая потенциал покоя, клетка «заряжается любовью».
Это любовь к двум вещам:
1) любовь клетки к калию,
2) любовь калия к свободе.
Как ни странно, но результат этих двух видов любви — пустота!
Именно она, пустота, создаёт в клетке отрицательный электрический заряд — потенциал покоя. Точнее, отрицательный потенциал создают пустые места, оставшиеся от убежавшего из клетки калия.
Итак, результат деятельности мембранных ионных насосов-обменников таков:
Натрий-калиевый ионный насос-обменник создаёт три потенциала (возможности):
1. Электрический потенциал — возможность затягивать внутрь клетки положительно заряженные частицы (ионы).
Электрический потенциал — возможность затягивать внутрь клетки положительно заряженные частицы (ионы).
2. Ионный натриевый потенциал — возможность затягивать внутрь клетки ионы натрия (и именно натрия, а не какие-нибудь другие).
3. Ионный калиевый потенциал — возможновть выталкивать из клетки ионы калия (и именно калия, а не какие-нибудь другие).
1. Дефицит натрия (Na+) в клетке.
2. Избыток калия (K+) в клетке.
Можно сказать так: ионные насосы мембраны создают разность концентраций ионов, или градиент (перепад) концентрации, между внутриклеточной и внеклеточной средой.
Именно из-за получившегося дефицита натрия в клетку теперь «полезет» этот самый натрий снаружи. Так всегда ведут себя вещества: они стремятся выравнять свою концентрацию во всём объёме раствора.
И в то же время в клетке получился избыток ионов калия по сравнению с наружной средой. Потому что насосы мембраны накачали его в клетку. И он стремится уравнять свою концентрацию внутри и снаружи, и поэтому стремится выйти из клетки.
Потому что насосы мембраны накачали его в клетку. И он стремится уравнять свою концентрацию внутри и снаружи, и поэтому стремится выйти из клетки.
Тут ещё важно понять, что ионы натрия и калия как бы «не замечают» друг друга, они реагируют только «на самих себя». Т.е. натрий реагирует на концентрацию натрия же, но «не обращает внимания» на то, сколько вокруг калия. И наоборот, калий реагирует только на концентрацию калия и «не замечает» натрий. Получается, что для понимания поведения ионов в клетке надо по-отдельности сравнивать концентрации ионов натрия и калия. Т.е. надо отдельно сравнить концентрацию по натрию внутри и снаружи клетки и отдельно — концентрацию калия внутри и снаружи клетки, но не имеет смысла сравнивать натрий с калием, как это часто делается в учебниках.
По закону выравнивания концентраций, который действует в растворах, натрий «хочет» снаружи войти в клетку. Но не может, так как мембрана в обычном состоянии плохо его пропускает. Его заходит немножко и клетка его опять тут же обменивает на наружный калий. Поэтому натрий в нейронах всегда в дефиците.
Поэтому натрий в нейронах всегда в дефиците.
А вот калий как раз может легко выходить из клетки наружу! В клетке его полно, и она его удержать не может. Так вот он и выходит наружу через особые белковые дырочки в мембране (ионные каналы).
АнализОт химического — к электрическому
А теперь — самое главное, следите за излагаемой мыслью! Мы должны перейти от движения химических частиц к движению электрических зарядов.
Калий заряжен положительным зарядом, и поэтому он, когда выходит из клетки, выносит из неё не только себя, но и «плюсики» (положительные заряды). На их месте в клетке остаются «минусы» (отрицательные заряды). Это и есть мембранный потенциал покоя!
Мембранный потенциал покоя — это дефицит положительных зарядов внутри клетки, образовавшийся за счёт утечки из клетки положительных ионов калия.
Заключение Рис. Схема формирования потенциала покоя (ПП). Автор благодарит Попову Екатерину Юрьевну за помощь в создании рисунка.
Автор благодарит Попову Екатерину Юрьевну за помощь в создании рисунка.
Составные части потенциала покоя
Потенциал покоя — отрицательный со стороны клетки и состоит как бы из двух частей.
1. Первая часть — это примерно -10 милливольт, которые получаются от неравносторонней работы мембранного насоса-обменника (ведь он больше выкачивает «плюсиков» с натрием, чем закачивает обратно с калием).
2. Вторая часть — это утекающий всё время из клетки калий, утаскивающий положительные заряды из клетки. Он дает большую часть мембранного потенциала, доводя его до -70 милливольт.
Калий перестанет выходить из клетки (точнее, его вход и выход сравняются) только при уровне электроотрицательности клетки в -90 милливольт. Но этому мешает постоянно подтекающий в клетку натрий, который тащит с собой свои положительные заряды. И в клетке поддерживается равновесное состояние на уровне -70 милливольт.
Так что всё дело в натрий-калиевом мембранном насосе-обменнике и последующем вытекании из клетки «лишнего» калия. За счёт потери положительных зарядов при этом вытекании внутри клетки нарастает электроотрицательность. Она-то и есть «мембранный потенциал покоя». Он измеряется внутри клетки и составляет обычно -70 мВ.
За счёт потери положительных зарядов при этом вытекании внутри клетки нарастает электроотрицательность. Она-то и есть «мембранный потенциал покоя». Он измеряется внутри клетки и составляет обычно -70 мВ.
Говоря образно, «мембрана превращает клетку в «электрическую батарейку» с помощью управления ионными потоками».
Мембранный потенциал покоя образуется за счёт двух процессов:
1. Работа калий-натриевого насоса мембраны.
Новая гипотеза механизма работы Na,K-АТФазы рассматривается здесь: Механизм натрий-калиевого насоса
Работа калий-натриевого насоса, в свою очередь, имеет 2 следствия:
1.1. Непосредственное электрогенное (порождающее электрические явления) действие ионного насоса-обменника. Это создание небольшой электроотрицательности внутри клетки (-10 мВ).
Виноват в этом неравный обмен натрия на калий. Натрия выбрасывается из клетки больше, чем поступает в обмен калия. А вместе с натрием удаляется и больше «плюсиков» (положительных зарядов), чем возвращается вместе с калием. Возникает небольшой дефицит положительных зарядов. Мембрана изнутри заряжается отрицательно (примерно -10 мВ).
Возникает небольшой дефицит положительных зарядов. Мембрана изнутри заряжается отрицательно (примерно -10 мВ).
1.2. Создание предпосылок для возникновения большой электроотрицательности.
Эти предпосылки — неравная концентрация ионов калия внутри и снаружи клетки. Лишний калий готов выходить из клетки и выносить из неё положительные заряды. Об этом мы скажем сейчас ниже.
2. Утечка ионов калия из клетки.
Из зоны повышенной концентрации внутри клетки ионы калия выходят в зону пониженной концентрации наружу, вынося заодно положительные электрические заряды. Возникает сильный дефицит положительных зарядов внутри клетки. В итоге мембрана дополнительно заряжается изнутри отрицательно (до -70 мВ).
Финал
Итак:
Калий-натриевый насос создает предпосылки для возникновения потенциала покоя. Это — разность в концентрации ионов между внутренней и наружной средой клетки. Отдельно проявляет себя разность концентрации по натрию и разность концентрации по калию. Попытка клетки выравнять концентрацию ионов по калию приводит к потере калия, потере положительных зарядов и порождает электроотрицательность внутри клетки. Эта электроотрицательность составляет большую часть потенциала покоя. Меньшую его часть составляет непосредственная электрогенность ионного насоса, т.е. преобладающие потери натрия при его обмене на калий.
Попытка клетки выравнять концентрацию ионов по калию приводит к потере калия, потере положительных зарядов и порождает электроотрицательность внутри клетки. Эта электроотрицательность составляет большую часть потенциала покоя. Меньшую его часть составляет непосредственная электрогенность ионного насоса, т.е. преобладающие потери натрия при его обмене на калий.
Видео: Мембранный потенциал покоя (Resting membrane potential)
© 2009-2021 Сазонов В.Ф. © 2016-2021 kineziolog.su
Электрическое поле. виды и работа. применение и свойства
Свойства
У каждого такого явления есть определенные особенности, которые постоянно остаются неизменными. Так, какова бы ни была энергетическая характеристика электрического поля, можно выделить следующие его свойства:
- Зрительно обнаружить такое явление невозможно, как и определить его параметры.
 Для этого необходимы специальные приборы.
Для этого необходимы специальные приборы. - Любое электрическое поле обладает некоторым воздействием на заряды, при помощи которых и возникает. Они же влияют на его обнаружение.
- Электрическое поле абсолютно реально и материально. Оно существовало и будет существовать вне зависимости от наших представлений, верований, знаний и так далее.
- Любое электрическое поле обладает такими характеристиками, как напряженность, потенциал и напряжение.
Современная наука уже умеет сознательно создавать такие явления и даже управлять ими в определенных пределах, но еще очень далека от того, чтобы полноценно поставить их на службу человеку.
Напряженность поля точечного заряда
Рассмотрим напряженность электрического поля уединенного точечного заряда либо заряженной сферы.
Из определения напряженности следует, что для случая взаимодействия двух точечных зарядов, зная силу их кулоновского взаимодействия, можем получить величину напряженности электрического поля, которое создается зарядом q в точке на расстоянии r от него до точки, в которой исследуется электрическое поле:
Данная формула показывает, что напряженность поля точечного заряда изменяется обратно пропорционально квадрату расстояния от данного заряда, то есть, например, при увеличении расстояния в два раза, напряженность уменьшается в четыре раза.
Линии напряженности
Попытаемся теперь охарактеризовать электростатическое поле нескольких зарядов. В этом случае необходимо воспользоваться сложением векторных величин напряженностей всех зарядов. Внесем пробный заряд и запишем сумму векторов сил, действующих на этот заряд. Результирующее значение напряженности получится при разделении значений этих сил на величину пробного заряда. Данный метод называется принципом суперпозиции.
Напряженность электростатического поля принято изображать графически при помощи силовых линий, которые также называют линиями напряженности. Такое изображение можно получить, построив вектора напряженности поля в как можно большем количестве точек вблизи данного заряда или целой системы заряженных тел.
Рис. 4. Линии напряженности электрического поля точечного заряда (Источник)
Рассмотрим несколько примеров изображения силовых линий. Линии напряженности выходят из положительного заряда (рис. 4,а), то есть положительный заряд является источником силовых линий.
Рассмотрим теперь систему, состоящую из положительного и отрицательного зарядов, находящихся на конечном расстоянии друг от друга (рис. 5). В этом случае линии напряженности направлены от положительного заряда к отрицательному.
Большой интерес представляет электрическое поле между двумя бесконечными плоскостями. Если одна из пластин заряжена положительно, а другая отрицательно, то в зазоре между плоскостями создается однородное электростатическое поле, линии напряженности которого оказываются параллельными друг другу (рис. 6).
Рис. 5. Линии напряженности системы двух зарядов (Источник)
Рис. 6. Линии напряженности поля между заряженными пластинами (Источник)
В случае неоднородного электрического поля величина напряженности определяется густотой силовых линий: там, где силовые линии гуще, величина напряженности поля больше (рис. 7).
Рис. 7. Неоднородное электрическое поле (Источник)
Определение: Линиями напряженности называют непрерывные линии, касательные к которым в каждой точке совпадают с векторами напряженности в этой точке.
Линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных и являются непрерывными.
Изображать электрическое поле с помощью силовых линий мы можем так, как сами посчитаем нужным, то есть число силовых линий, их густота ничем не ограничивается. Но при этом необходимо учитывать направление векторов напряженности поля и их абсолютные величины.
Очень важно следующее замечание. Как говорилось ранее, закон Кулона применим только для точечных покоящихся зарядов, а также заряженных шариков, сфер
Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает.
Список литературы
- Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2008.
- Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000.
- Рымкевич А.П. Физика. Задачник.
 10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.
10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013. - Генденштейн Л.Э., Дик Ю.И. Физика. 10 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (базовый уровень) – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Nauka.guskoff.ru (Источник).
- Youtube (Источник).
- Physics.ru (Источник).
Домашнее задание
- Стр. 378: № 1–3. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000. (Источник)
- С каким ускорением движется электрон в поле напряженностью 10 кВ/м?
- В вершинах равностороннего треугольника со стороной a находятся заряды +q, +q и –q. Найти напряженность поля Е в центре треугольника.
Определение
Вокруг заряженного тела возникает электрическое поле. Если сказать формулировку простыми словами, то это такое поле, которое действует на другие тела с определенной силой.
Основной количественной характеристикой является напряженность электрического поля. Она равна отношению силы, действующей на заряд, к величине заряда. Сила действует в каком-то направлении, значит и напряженность ЭП векторная величина. Ниже вы видите формулу напряженности:
Она равна отношению силы, действующей на заряд, к величине заряда. Сила действует в каком-то направлении, значит и напряженность ЭП векторная величина. Ниже вы видите формулу напряженности:
Напряженность ЭП действует в направлении, которое вычисляется по принципу суперпозиции. То есть:
На рисунке ниже вы видите условное графическое изображение двух зарядов разной полярности и силовые линии электрического поля, возникающего между ними.
Важно! Главным условием возникновения электрического поля является то, что тело должно иметь какой-то заряд. Только тогда вокруг него возникнет поле, которое будет действовать на другие заряженные тела
Чтобы определить величину напряженности электрического поля вокруг единичного пробного заряда используют закон Кулона, в этом случае:
Такое поле называют еще и кулоновским.
Другой важной физической величиной является потенциал электрического поля. Это уже не векторная, а скалярная величина, она прямопропорциональна энергии, приложенной к заряду:
Важно! Силовой и энергетической характеристикой электрического поля является напряженность и потенциал. Это и есть его основные физические свойства
Это и есть его основные физические свойства
Он измеряется в Вольтах и численно равен работе ЭП по перемещению заряда из определенной точки в бесконечность.
Более подробно узнать о том, что такое напряженность электрического поля, вы можете из видео урока:
Примечания
- // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если E→{\displaystyle {\vec {E}}} одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия E→{\displaystyle {\vec {E}}} в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.

- Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле E→{\displaystyle {\vec {E}}} — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
- Хотя исторически многие из них были открыты раньше.
Практика
Мы уже упомянули о том, что в быту электрическое поле проявляется, когда вы снимаете шерстяную или синтетическую одежду с себя и проскакивают искорки между волосами и шерстью, когда натрете пластиковую линейку и проведете над мелкими бумажками, а они притягиваются и прочее. Но это не является нормальными техническими примерами.
В проводниках малейшее ЭП вызывает движение носителей зарядов и их перераспределение. В диэлектриках, так как ширина запрещенной зоны в этих веществах большая, ЭП вызовет движение носителей зарядов только в случае пробоя диэлектрика. В полупроводниках действие находится между диэлектриком и проводником, но нужно преодолеть небольшую ширину запрещенной зоны, передав энергию порядка 0.3…0.7 эВ (для германия и кремния).
В диэлектриках, так как ширина запрещенной зоны в этих веществах большая, ЭП вызовет движение носителей зарядов только в случае пробоя диэлектрика. В полупроводниках действие находится между диэлектриком и проводником, но нужно преодолеть небольшую ширину запрещенной зоны, передав энергию порядка 0.3…0.7 эВ (для германия и кремния).
Из того, что есть в каждом доме – это электронные бытовые приборы, в том числе и блоки питания. В них есть важная деталь, которая работает благодаря электрическому полю – это конденсатор. В нём заряды удерживаются на обкладках, разделенных диэлектриком, как раз таки благодаря работе электрического поля. На картинке ниже вы видите условное изображение зарядов на обкладках конденсатора.
Другое применение в электротехнике — это полевые транзисторы или МДП-транзисторы. В их названии уже упоминается принцип действия. В них принцип работы основан на изменении проводимости СТОК-ИСТОК под воздействием на полупроводник поперечного электрического поля, а в МДП (МОП, MOSFET – одно и то же) и вовсе затвор отделен диэлектрическим слоем (окислом) от проводящего канала, так что влияние токов ЗАТВОР-ИСТОК невозможно по определению.
Другое применение уже отошедшее в быту, но еще «живое» в промышленной и лабораторной технике – электроннолучевые трубки (ЭЛТ или т.н. кинескопы). Где одним из вариантов устройства для перемещения луча по экрану является электростатическая отклоняющая система.
Если рассказать простым языком, то есть пушка, которая излучает (эмитирует) электроны. Есть система, которая отклоняет этот электрон в нужную точку на экране, для получения необходимого изображения. Напряжение прикладывается к пластинам, а на эмитированный летящий электрон воздействуют кулоновские силы, соответственно и электрическое поле. Все описанное происходит в вакууме. Тогда к пластинам прикладывают высокое напряжение, а для его формирования устанавливают трансформатор строчной развертки и обратноходовой преобразователь.
На видео ниже кратко и понятно объясняется, что такое электрическое поле и какими свойствами обладает этот особый вид материи:
youtube.com/embed/DzhxrX117TU?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Материалы по теме:
- Что такое диэлектрические потери
- Зависимость сопротивления проводника от температуры
- Закон Ома простыми словами
- Книги для электриков
Основные характеристики
Их можно описать при помощи математических закономерностей, а некоторые — выразить графически. Последние характеристики являются векторными, то есть имеющими направление
Это важно, поскольку при решении практических задач часто приходится оперировать не модулем величины, а проекцией вектора на какую-либо выбранную ось
Основными параметрами поля являются:
- напряженность;
- потенциал;
- индукция.
Напряженность поля
Это силовая характеристика электрического поля. Величина это векторная, и она характеризует силу, с которой поле воздействует на заряд в конкретной точке. Математически это выражается так:
Математически это выражается так:
Ē = F̄/q.
Если подставить сюда формулу закона Кулона, то получим:
Ē = q₀ / 4 π ε ε₀ r ².
Если поле создано двумя зарядами, то результирующая напряженность рассчитывается графически — при помощи сложения векторов напряженностей от каждого отдельного источника. Этот способ получил название принципа суперпозиции.
Потенциалы и их разность
Электрическое поле способно совершать работу. Если пробный заряд передвигать в поле, то работа, выполненная эл. полем, будет зависеть от начального и конечного расстояние от пробного заряда до центра эл. поля. Сравнить это можно с человеком, который собрался прыгать с крыши. Пока он находится на высоте десятого этажа, его потенциальная энергия будет равна:
W = -GMm / Rr.
Или если учесть соразмерность земли и человека:
W = mgh.
Пока человек не прыгнул, он обладает потенциальной энергией. Когда же он, наконец, упадет, гравитационное поле совершит работу, численно равную вышеуказанной величине. При этом не учитывается горизонтальное перемещение — эту работу совершал сам покойный.
W = q₁ q₀ / 4 π ε ε₀ r.
При перемещении в другую точку, когда расстояние r будет иным, поле совершит работу, равную:
A = W₁ — W₂ = q₁ q₀ /4 π ε ε₀ r₁ — q₁ q₀ / 4 π ε ε₀ r₂.
Если из обоих слагаемых выделить параметр, который относится непосредственно к полю, а не к пробному заряду, он будет выглядеть так:
φ₁ = q₀ /4 π ε ε₀ r₁; φ₂ = q₀ / 4 π ε ε₀ r₂.
И вот это φ и называется потенциалом поля в точке. Исходя из всех написанных выше формул, можно выразить эту величину так:
φ ₁ = W₁ / q₁; φ₂ = W₂ / q₁.
Таким образом, работа, которую совершит поле, будет выражена следующим образом:
A = W₁ — W₂ = φ₁ q₁ — φ₂ q₁ = q₁ (φ₁ — φ₂).
Выражение в скобках будет называться разностью потенциалов, или напряжением. Она показывает, какую работу совершит поле по перемещению пробного заряда.
A/q = (φ₁ — φ₂).
Единица этой величины, Дж/Кл, получила название Вольт, в честь ученого Алессандро Вольта. От этой единицы отсчитывают размерность и других величин в электростатике и электродинамике. Например, напряженность поля измеряется в В/м.
Электрическая индукция
Эта величина характеризует электрическое поле, что называется, в чистом виде. В реальности мы имеем дело с полем в различных средах, имеющих определенную диэлектрическую проницаемость. Несмотря на то что для большинства веществ это табличная величина, в ряде случаев она непостоянна, а ее зависимость от параметров среды (температура, влажность и т. д. ) нелинейна.
В реальности мы имеем дело с полем в различных средах, имеющих определенную диэлектрическую проницаемость. Несмотря на то что для большинства веществ это табличная величина, в ряде случаев она непостоянна, а ее зависимость от параметров среды (температура, влажность и т. д. ) нелинейна.
Такое явление характерно для сегнетовой соли, титаната бария, ниобата лития и ряда других.
D = ε ε₀ E.
Это тоже векторная величина, направление которой совпадает с направлением напряженности.
Применение
Характеристики электрических полей подразумевают наличие двух основных свойств, которые и используются человеком. Так, они могут формировать ионы, а погруженные в жидкость электроды позволяют без особых усилий разделять ее, грубо говоря, по фракциям. Именно в основе этих свойств и лежит использование электрических полей.
- Медицина. Тут применяется система воздействия на пораженное место направленными ионами. В результате они способствуют повышению скорости регенерации, очищают рану, убивают микробов и так далее. Кроме того, свойства и характеристики электрических полей позволяют им «вибрировать» с большой частотой. Эта особенность также используется. Благодаря ей можно повысить температуру некоторых отдельных частей тела, что будет способствовать улучшению кровотока и положительно скажется на здоровье.
- Очистка. В этой сфере используется система разделения жидкостей. Так, именно подобная особенность применяется в очистных сооружениях. Вода, в которой растворено огромное количество всевозможного мусора, становится очень вредной. При этом с ней сложно что-то сделать, ведь далеко не все фильтры смогут справиться с проблемой. В такой ситуации и применяются электрические поля, которые разделяют воду, отделяя от нее часть загрязнений. В результате получается достаточно простой, быстрый и дешевый этап очистки.
- Химия. Эта наука использует в промышленности то же самое свойство разделения жидкостей. Оно активно применяется в лабораторных условиях, но чаще всего его можно встретить в сфере добычи нефти. В некоторых случаях она получается достаточно загрязненной и требуется потратить много времени средств, чтобы в конечном итоге возник нужный продукт. Справиться с этим сильно помогает электрическое поле. Оно разделяет нефть, убирая большую часть загрязняющих элементов и тем самым значительно облегчая ее дальнейшую обработку.
Существует и множество других вариантов использования. Например, электромагнитное поле, в состав которого входит и рассматриваемое в этой статье явление, может служить беспроводной системой передачи электричества к разным приборам. К сожалению, в большинстве случаев все подобные разработки носят скорее теоретический и экспериментальный характер.
Статическое и вихревое поле
Как упоминалось в начале статьи, электрическое поле может возникать вокруг переменного магнитного поля. Оно даже создает ток, что может быть достигнуто двумя путями:
- изменением интенсивности магнитного поля, проходящего сквозь контур проводника в нем;
- изменением положения самого проводника.
При этом проводнику вовсе не обязательно быть замкнутым — ток в нем все равно будет течь.
Для иллюстрации отличий статического и вихревого поля можно составить таблицу.
| Параметр | Электростатическое | Вихревое |
| форма силовых линий | разомкнутые | замкнутые |
| чем создается | неподвижным зарядом | переменным магнитным потоком |
| источник напряженности | заряд | отсутствует |
| работа по перемещению в замкнутом контуре | нулевая | создает ЭДС индукции |
Нельзя сказать, что первое и второе поле никак между собой не связаны. Это не так. В реальности работает такая закономерность: неподвижный заряд создает электростатическое поле, которое движет заряд в проводнике; движущийся заряд порождает постоянное магнитное поле. Если заряд движется с непостоянной скоростью и направлением, то магнитное поле становится переменным и создает вторичное электрическое. Таким образом, электрическое поле и его характеристики влияют на возможность возникновения магнитного и его параметры.
Характеристики электрического поля
Электрическое поле описывается векторной величиной – напряженностью. Стрелка, направление которой совпадает с силой, действующей в точке на единичный положительный заряд, длина пропорциональна модулю силы. Физики находят удобным пользоваться потенциалом. Величина скалярная, проще представить на примере температуры: в каждой точке пространства некоторое значение. Под электрическим потенциалом понимают работу, совершаемую для перемещения единичного заряда из точки нулевого потенциала в данную точку.
Электрический потенциал
Поле, описываемое указанным выше способом, называется безвихревым. Иногда именуют потенциальным. Функция потенциала электрического поля непрерывная, изменяется плавно по протяженности пространства. В результате выделим точки равного потенциала, складывающие поверхности. Для единичного заряда сфера: дальше объект, слабее поле (закон Кулона). Поверхности называют эквипотенциальными.
Для понимания уравнений Максвелла заимейте представление о нескольких характеристиках векторного поля:
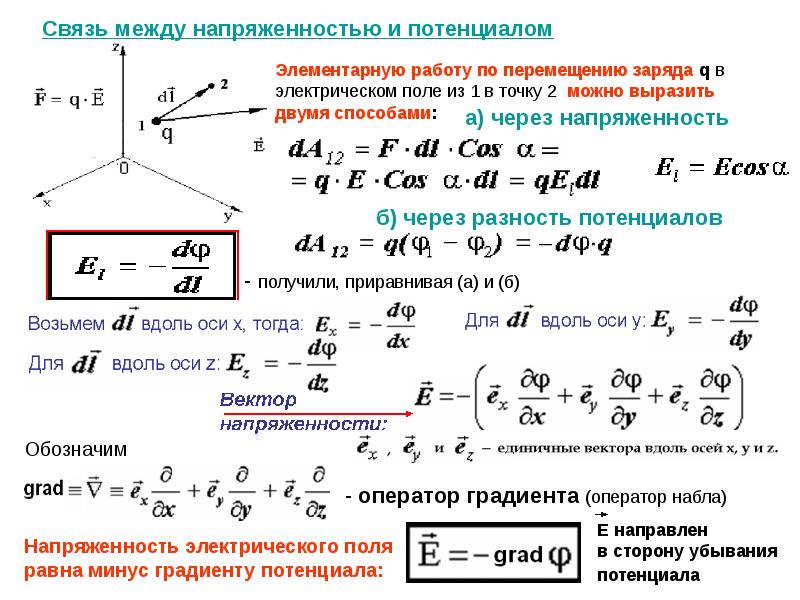
Градиентом электрического потенциала называется вектор, направление совпадает с наискорейшим ростом параметра поля. Значение тем больше, чем быстрее изменяется величина. Направлен градиент от меньшего значения потенциала к большему:
- Градиент перпендикулярен эквипотенциальной поверхности.
- Градиент тем больше, чем ближе расположение эквипотенциальных поверхностей, отличающихся друг от друга на заданную величину потенциала электрического поля.
- Градиент потенциала, взятый с обратным знаком, является напряженностью электрического поля.
Электрический потенциал. Градиент “взбирается в гору”
- Дивергенция является скалярной величиной, вычисляемой для вектора напряженности электрического поля. Является аналогом градиента (для векторов), показывает скорость изменения величины. Необходимость во введении дополнительной характеристики: векторное поле лишено градиента. Следовательно, для описания требуется некий аналог – дивергенция. Параметр в математической записи схож с градиентом, обозначается греческой буквой набла, применяется для векторных величин.
- Ротор векторного поля именуется вихрем. Физически величина равна нулю при равномерном изменении параметра. Если ротор отличен от нуля, возникают замкнутые изгибы линий. У потенциальных полей точечных зарядов по определению вихрь отсутствует. Не обязательно линии напряжённости в этом случае прямолинейны. Просто изменяются плавно, не образуя вихрей. Поле с ненулевым ротором часто называют соленоидальным. Часто применяется синоним – вихревое.
- Полный поток вектора представлен интегралом по поверхности произведения напряженности электрического поля на элементарную площадь. Предел величины при стремлении емкости тела к нулю представляет собой дивергенцию поля. Понятие предела изучается старшими классами средней школы, ученик может составить некоторое представление на предмет обсуждения.
Уравнения Максвелла описывают изменяющееся во времени электрическое поле и показывают, что в таких случаях возникает волна. Принято считать, одна из формул указывает отсутствие в природе обособленных магнитных зарядов (полюсов). Иногда в литературе встретим особый оператор – лапласиан. Обозначается как квадрат набла, вычисляется для векторных величин, представляет дивергенцией градиента поля.
Подобные аксиомы легко положим в основу описания процессов, происходящих в реальных существующих устройствах. Антигравитационный, вечный двигатель были бы неплохим подспорьем экономике. Если реализовать на практике теорию Эйнштейна никому не удалось, наработки Николы Тесла исследуются энтузиастами. Отсутствуют ротор, дивергенция.
Электризация тел
Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.
Способы электризации:
- трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
- через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
- при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
- при ударе;
- под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.
Потенциал
Это еще одна характеристика электрического поля. Потенциал является накопленной энергией, которую явление может использовать для перемещения зарядов. Когда тот начинает двигаться, на это тратится вот этот самый ресурс, и в конечном итоге он становится равным нулю. Накапливается он обратным образом. В качестве примера можно взять все тот же заряд, но расположенный вне электрического поля. Как только некая сила перемещает его внутрь и двигает там, появляется потенциал.
Проще всего это представить на примере обычной пружины. В своем спокойном положении она не имеет никакого потенциала и просто представляет собой изогнутый кусок металла. Но как только мы начнем сдавливать ее, начнет возникать потенциал. Если отпустить пружину, она моментально распрямится и при этом подвинет все предметы, которые сможет, расположенные на ее пути. Если вернуться к рассматриваемым электрическим полям, то в их случае потенциал будет строго соответствовать приложенным усилиям на перемещение заряда. В современной науке этот показатель измеряется вольтами.
Что такое электрическое поле
Как и во многих других случаях, начать описание данного явления нужно именно с его определения. С точки зрения современной науки, оно представляет собой специальный вариант материи, созданной при помощи заряженных тел. Обнаружить электрическое поле и его характеристики можно благодаря взаимодействию друг с другом зарядов. Они и есть основные составные элементы данного явления. Обычным зрением обнаружить его невозможно, но у человека много других органов чувств. И вот с их помощью определить наличие такого поля вполне реально. Самый простой пример – поднести руку к экрану телевизора. Он, как и любые другие электронные приборы, создает вокруг себя именно такое поле, на что реагируют волоски на руке. В результате человек получает возможность весьма условно, но все же определять наличие или отсутствие такого явления.
Электрическое поле
Закон Кулона, изученный на прошлом уроке, был установлен экспериментально и справедлив для покоящихся заряженных тел. Каким же образом происходит взаимодействие заряженных тел на расстоянии? До некоторых пор при изучении электрических взаимодействий бок о бок развивались две принципиально разные теории: теория близкодействия и теория дальнодействия (действия на расстоянии).
Теория близкодействия заключается в том, что заряженные тела взаимодействуют друг с другом посредством промежуточного звена (например, цепь в задаче о поднятии ведра из колодца является промежуточным звеном, посредством которого мы воздействуем на ведро, то есть поднимаем его).
Теория дальнодействия гласит, что заряженные тела взаимодействуют через пустоту. Шарль Кулон придерживался именно этой теории и говорил, что заряженные тела «чувствуют» друг друга. В начале XIX века конец спорам положил Майкл Фарадей (рис. 1). В работах, связанных с электрическим полем, он установил, что между заряженными телами существует некий объект, который и осуществляет действие заряженных тел друг на друга. Работы Майкла Фарадея были подтверждены Джеймсом Максвеллом (рис. 2). Он показал, что действие одного заряженного тела на другое распространяется за конечное время, таким образом, между заряженными телами должно существовать промежуточное звено, через которое осуществляется взаимодействие.
Рис. 1. Майкл Фарадей (Источник)
Рис. 2. Джеймс Клерк Максвелл (Источник)
Определение: Электрическое поле – это особая форма материи, которая создается покоящимися зарядами и определяется действием на другие заряды.
Коррозия для блондинок -начало
Чтобы понять, попробуй объяснить это простыми словамиПортреты протекторов этого года, отработавших в общей сложности 10 месяцев (два сезона), правый борт — корма, нос, левый борт — корма, нос. Разницу видно невооруженным взглядом.
Почему аноды разрушились по-разному?
Каждый раз, поднимаясь из воды, катерщики и парусники озабоченно изучают свои полуразрушенные (или нетронутые) цинковые аноды, делая какие-то только им известные выводы. Некоторые соединяют электрическими проводами все металлические детали своих «пароходов», другие, наоборот, изолируют все, что можно, а третьи вообще не обращают на это внимания, просто меняют изношенные аноды и испорченные узлы. Теория гальванической коррозии не является тайной, практическоие рекомендации общеизвестны, но «дьявол кроется в деталях», которые иногда приводят к неожиданным результатам.
Далее — практическое расследование некоторых особенностей коррозии металлов в морской воде, естественно, с шаманством и заклинанием духов.
Содержание статьи
Начнем с самого начала, с
электрохимического ряда напряжений металлов.Еще в школе нас знакомили с такой особенностью окружающего мира, что каждый металл имеет собственный электрический потенциал, что нет металлов с одинаковым потенциалом, и что при погружении в электролит электродов из разных металлов между ними возникает разность электрических потенциалов, которую можно измерить чувствительным вольтметром. На этом теоретическую часть мы закончим, и перейдем к практике.
Классический школьный ряд напряжений с точки зрения моряка, нам не очень подходит, однако есть практические таблицы — «Galvanic Series in Metals in Seawater». Во-первых, в них использованы результаты измерения потенциалов металлов и сплавов, используемых при строительстве судов, во-вторых, в качестве электролита применялась проточная морская вода — при температурах от +10 до +27 градусов Цельсия, и скоростях потока 5 — 8 узлов.
Что все это значит с точки зрения нашей морской практики и как это можно применить?
Первое, что бросается в глаза при анализе этой таблицы — довольно заметная разность электрических потенциалов у «обычной» углеродистой стали и «нержавейки». Цифры — цифрами, но для ясного понимания, ну, и, конечно, «из любви к искусству» напрашивается эксперимент, для которого понадобятся образцы деталей нашей лодки, вольтметр с приличным входным сопротивлением, и банка свежей морской воды.
продолжение следует — нужна вода…
Страница 1 из 14 В. В. Мантуров
Мы продолжим разговор о (магнитном) векторном потенциале. Говорят (и давно), что это передний край науки. Есть ли основания для такой оценки? Есть. Показано, что векторный потенциал обладает и определенностью, и однозначностью, и измеримостью, и силовыми свойствами. Показано, насколько многоаспектны и многогранны проявления векторного потенциала как в электродинамике классической, так и квантовой. И это будут только те факты, явления и эффекты, в суть лишь которых автору удалось чуть-чуть проникнуть. Настало, по-видимому, время признать, что описание электромагнитных явлений с помощью векторного потенциала несет больше информации, чем с помощью электромагнитных напряженностей, и более удобно в работе.
О векторном потенциале интуитивно и объективно О векторном потенциале физики спорят давно. Большинство сходятся на том, что векторный потенциал – не более чем удобный математический символ, ибо он не обладает ни определенностью, ни однозначностью, ни измеримостью, ни силовыми качествами, и потому предпочитают пользоваться давно проверенными напряженностью электрического поля и индукцией магнитного. Потенциалами обычно манипулируют (тем они и удобны) при решении дифференциальных уравнений. Изредка [19] говорят даже “об особой роли”. Электродинамику мы начинаем осваивать со школьной скамьи. А закрепляем эти сведения в результате использования электротехники, радиотехники и электроники. Но все эти пути нашего познания приводят к тому, что электрическое поле мы связываем с его напряженностью, разностью потенциалов и силой тока, а, говоря о магнитном поле, мы имеем в виду его индукцию или напряженность. А между тем еще Фарадей [1] мучился сомнениями по поводу выдвинутой им самим же гипотезы об электротоническом состоянии, которое, как он полагал, всегда существует в пространстве. Говоря об индуктивном действии, он писал –(§ 1661):”…вероятно, то, что действует на проводник, будет действовать и на изолятор, производя в нем, может быть, нечто, чему можно дать название элекротонического состояния…”. Под «изолятором» он имел в виду и воздух, т.е. вакуум. И всегда, следовательно, это состояние находится в полной готовности отреагировать, откликнуться, на изменение ситуации относительно преимущественно проводящих тел, находящихся и движущихся в электромагнитном поле. Да, да. Имеется в виду, что Фарадей в своей гипотезе об электротоническом состоянии еще в те времена интуитивно догадывался о том, что явления индукции не обходятся без “вмешательства”, как теперь понятно, потенциалов (электромагнитных): векторного потенциала и скалярного. Он гениально догадывался именно о подспудном действии векторного потенциала [1, (§§ 60-75, 243, 1114, 1661, 1662, 1731,…)]. Он также понимал, что электротоническое состояние тесно и непосредственно связано с магнитным полем, с проявлениями индуктивности, но и к электрическому бывает очень даже причастно. Максвелл [2] уловил эту догадку Фарадея и посвятил ей свой трактат «О фарадеевых силовых линиях», в котором часть 11 так и названа «О фарадеевом «электротоническом состоянии». См. также [2, сс 107-114, 127-137, 142-147 и т.д.]. Больше того, догадку Фарадея он развил и воплотил в своей идее о токе смещения в [2, глава 1Х]. И делал он это целенаправленно: “… Может показаться, что я не отдал должного воззрениям многих выдающихся ученых электриков и математиков. Одна из причин этого состоит в том, что, прежде чем начать изучение электричества, я решил не читать никаких математических работ по этому предмету до тщательного прочтения мной «Экспериментальных исследований в области электричества» Фарадея. Я знал, что между пониманием явлений Фарадеем и концепцией математиков предполагалось наличие такой разницы, что ни тот, ни другие не были удовлетворены языком друг друга. Я был убежден также, что расхождение это возникало не из-за неправоты какой-либо сторон. Впервые меня убедил в этом сэр Вильям Томсон” [2, с 348-3]. ПерваяПредыдущая 1 2 3 4 5 6 7 8 9 10 Следующая > Последняя >> |
Трёхфазный ток, преимущества трёхфазного тока при использовании
Преимущества трёхфазного тока очевидны только специалистам электрикам. Что такое трехфазный ток для обывателя представляется весьма смутно. Давайте развеем неопределенность.
Трехфазный переменный ток
Большинство людей, за исключением специалистов — электриков, имеют весьма смутное представление, что такое так называемый «трёхфазный» переменный ток, да и в понятиях, что такое сила тока, напряжение и электрический потенциал, а также мощность, — часто путаются.
Попытаемся простым языком дать начальные понятия об этом. Для этого обратимся к аналогиям. Начнём с простейшей – протекания постоянного тока в проводниках. Его можно сравнить с водным потоком в природе. Вода, как известно, всегда течёт от более высокой точки поверхности к более низкой. Всегда выбирает самый экономичный (наикратчайший) путь. Аналогия с протеканием тока – полнейшая. Причём количество воды протекающей в единицу времени через какое-то сечение потока будет аналогично силе тока в электрической цепи. Высота любой точки русла реки относительно нулевой точки – уровня моря – будет соответствовать электрическому потенциалу любой точки цепи. А разница в высоте любых двух точек реки будет соответствовать напряжению между двумя точками цепи.
Используя эту аналогию можно легко представить в уме законы протекания постоянного электрического тока в цепи. Чем выше напряжение – перепад высот, тем больше скорость потока, и, следовательно, количество воды протекающей по реке в единицу времени.
Водный поток, точно так же как электрический ток при своём движении испытывает сопротивление русла – по каменистому руслу вода будет протекать бурно, меняя направление, немного нагреваясь от этого (бурные потоки даже в сильные морозы не замерзают вследствие нагрева от сопротивления русла). В гладком канале или трубе вода потечёт быстро и в итоге в единицу времени канал пропустит гораздо больше воды, чем извилистое и каменистое русло. Сопротивление потоку воды полностью аналогично электрическому сопротивлению в цепи.
Теперь представим закрытую бутылку, в которой налито немного воды. Если мы начнём эту бутылку вращать вокруг поперечной оси, то вода в ней будет перетекать попеременно от горлышка к донышку и наоборот. Это представление – аналогия переменному току. Казалось бы, одна и та же вода перетекает туда-сюда и что? Тем не менее, этот переменный поток воды способен совершать работу.
Откуда вообще появилось понятие переменный ток? к содержанию
Да с тех самых пор, когда человечество, узнав, что перемещение магнита вблизи проводника вызывает электрический ток в проводнике. Именно движение магнита вызывает ток, если магнит положить рядом с проводом и не двигать – никакого тока в проводнике это не вызовет. Далее, мы хотим получить (генерировать) в проводнике ток, чтобы использовать его в дальнейшем для каких-либо целей. Для этого изготовим катушку из медного провода и начнём возле неё двигать магнит. Магнит можно передвигать возле катушки как угодно – двигать по прямой туда-сюда, но, чтобы не двигать магнит руками, создать такой механизм технически сложнее, чем просто начать его вращать около катушки, аналогично вращению бутылки с водой из предыдущего примера. Вот именно таким образом — по техническим причинам — мы и получили синусоидальный переменный ток, используемый ныне повсеместно. Синусоида – это развёрнутое во времени описание вращения.
В дальнейшем оказалось, что законы протекания переменного тока в цепи отличаются от протекания постоянного тока. Например, для протекания постоянного тока сопротивление катушки равно просто омическому сопротивлению проводов. А для переменного тока – сопротивление катушки из проводов значительно увеличивается из-за появления, так называемого индуктивного сопротивления. Постоянный ток через заряженный конденсатор не проходит, для него конденсатор – разрыв цепи. А переменный ток способен свободно протекать через конденсатор с некоторым сопротивлением. Далее выяснилось, что переменный ток может быть преобразован с помощью трансформаторов в переменный ток с другими напряжением или силой тока. Постоянный ток такой трансформации не поддаётся и, если мы включим любой трансформатор в сеть постоянного тока (что делать категорически нельзя), то он неизбежно сгорит, так как постоянному току будет сопротивляться только омическое сопротивление провода, которое делается как можно меньше, и через первичную обмотку потечёт большой ток в режиме короткого замыкания.
Заметим также, что электродвигатели могут быть созданы для работы и от постоянного тока, и от переменного тока. Но разница между ними такая – электродвигатели постоянного тока сложнее в изготовлении, но зато позволяют плавно изменять скорость вращения обычным регулирующим силу тока реостатом. А электродвигатели переменного тока гораздо проще и дешевле в изготовлении, но вращаются только с одной, обусловленной конструкцией скоростью. Поэтому в практике широко применяются и те, и другие. В зависимости от назначения. Для целей управления и регулирования применяются двигатели постоянного тока, а в качестве силовых установок – двигатели переменного тока.
Далее конструкторская мысль изобретателя генератора двигалась примерно в таком направлении – если удобнее всего для генерации тока использовать вращение магнита рядом с катушкой, то почему бы вместо одной катушки генератора не расположить вокруг вращающегося магнита несколько катушек (места-то вокруг вон сколько)?
Получится сразу же, как бы несколько генераторов, работающих от одного вращающегося магнита. Причём переменный ток в катушках будет отличаться по фазе – максимум тока в последующих катушках будет несколько запаздывать относительно предыдущих. То есть синусоиды тока, если их графически изобразить, будут, как бы между собой, сдвинуты. Это важное свойство – сдвиг фаз, о котором мы расскажем ниже.
Примерно так рассуждая, американский изобретатель Никола Тесла и изобрёл сначала переменный ток, а затем и трёхфазную систему генерации тока с шестью проводами. Он расположил три катушки вокруг магнита на равном расстоянии под углами 120 градусов, если за центр углов принять ось вращения магнита.
(Число катушек (фаз) вообще-то может быть любым, но для получения всех тех преимуществ, что даёт многофазная система генерации тока, минимально достаточно трёх).
Далее русский учёный электротехник Михаил Осипович Доливо-Добровольский развил изобретение Н. Тесла, впервые предложив трёх — и четырёхпроводную систему передачи трёхфазного переменного тока. Он предложил соединить один конец всех трёх обмоток генератора в одну точку и передавать электроэнергию всего по четырём проводам. (Экономия на дорогих цветных металлах существенная). Оказалось, что при симметричной нагрузке каждой фазы (равным сопротивлением) ток в этом общем проводе равняется нулю. Потому что при суммировании (алгебраическом, с учётом знаков) сдвинутых по фазе на 120 градусов токов они взаимно уничтожаются. Этот общий провод так и назвали – нулевой. Поскольку ток в нём возникает только при неравномерности нагрузок фаз и численно он небольшой, гораздо меньше фазных токов, то представилась возможность использовать в качестве «нулевого» провод меньшего сечения, чем для фазных проводов.
По этой же самой причине (сдвиг фаз на 120 градусов) трехфазные трансформаторы получились значительно менее материалоёмкими, так как в магнитопроводе трансформатора происходит взаимопоглощение магнитных потоков и его можно делать с меньшим сечением.
Сегодня трёхфазная система электроснабжения осуществляется четырьмя проводами, три из них называются фазными и обозначаются латинскими буквами: на генераторе — А, В и С, у потребителя — L1, L2 и L3. Нулевой провод так и обозначается – 0.
Напряжение между нулевым проводом и любым из фазных проводов называется – фазным и составляет в сетях потребителей – 220 вольт.
Между фазными проводами тоже существует напряжение, причём значительно выше, чем фазное напряжение. Это напряжение называется линейным и составляет в цепях потребителей 380 вольт. Почему же оно больше фазного? Да всё это из-за сдвига фаз на 120 градусов. Поэтому, если на одном проводе, к примеру, в данный момент времени потенциал равен плюс 200 вольт, то на другом фазном проводе в этот же момент времени потенциал будет минус 180 вольт. Напряжение – это разность потенциалов, то есть оно будет + 200 – (-180)=+380 В.
Возникает вопрос, если по нулевому проводу ток не протекает, то нельзя ли его вообще убрать. Можно. И мы получим трёхпроводную систему электроснабжения. С соединением потребителей так называемым «треугольником» — между фазными проводами. Однако нужно заметить, что при неравномерной нагрузке в сторонах «треугольника» на генератор будут действовать разрушающие его нагрузки, поэтому данную систему можно применять при огромном количестве потребителей, когда неравномерности нагрузок нивелируются. Передача электроэнергии от больших электростанций при высоких фазных и линейных напряжениях (сотни тысяч вольт) так и осуществляются. Почему же применяется такое высокое напряжение. Ответ простой – чтобы уменьшить потери в проводах на нагрев. Так как нагрев проводов (потери энергии) пропорционален квадрату протекающего тока, то желательно чтобы протекающий ток был минимален. Ну а для передачи необходимой мощности при минимальном токе нужно повышать напряжение. Линии электропередач (ЛЭП) так и обозначаются, к примеру, ЛЭП – 500 – это линия электропередачи под напряжением 500 киловольт.
Кстати потери в проводах ЛЭП можно ещё более снизить, применяя передачу постоянного тока высокого напряжения (перестаёт действовать емкостная составляющая потерь, действующая между проводами), проводились даже такие эксперименты, но широкого распространения пока такая система не получила, видимо вследствие большей экономии в проводах при трёхфазной системе генерации.
Выводы: преимущества трёхфазной системы к содержанию
В заключение статьи подведём итоги, – какие же преимущества даёт трёхфазная система генерации и электроснабжения?
- Экономия на количестве проводов, необходимых для передачи электроэнергии. Учитывая немалые расстояния (сотни и тысячи километров) и то, что для проводов используют цветные металлы с малым удельным электрическим сопротивлением, экономия получается весьма существенной.
- Трёхфазные трансформаторы, при равной мощности с однофазными, имеют значительно меньшие размеры магнитопровода. Что позволяет получить существенную экономию.
- Очень важно, что трёхфазная система передачи электроэнергии создаёт при подключении потребителя к трём фазам как бы вращающееся электромагнитное поле. Опять-таки, вследствие сдвига фаз. Это свойство позволило создать чрезвычайно простые и надёжные трёхфазные электродвигатели, у которых нет коллектора, а ротор, по сути, представляет собой простую «болванку» в подшипниках, к которой не нужно подсоединять никакие провода. (На самом деле конструкция короткозамкнутого ротора имеет свои особенности и вовсе не болванка) Это так называемые трёхфазные асинхронные электродвигатели с короткозамкнутым ротором. Очень широко распространённые сегодня в качестве силовых установок. Замечательное свойство таких двигателей – это возможность менять направление вращения ротора на обратное простым переключением двух любых фазных проводов.
- Возможность получения в трёхфазных сетях двух рабочих напряжений. Другими словами менять мощность электродвигателя или нагревательной установки путём простого переключения питающих проводов.
- Возможность значительного уменьшения мерцаний и стробоскопического эффекта светильников на люминисцентных лампах путём размещения в светильнике трёх ламп, питающихся от разных фаз.
Благодаря этим преимуществам трёхфазные системы электроснабжения получили широчайшее распространение в мире.
Электрический потенциал — Простая английская Википедия, бесплатная энциклопедия
Электрический потенциал — это электрическая потенциальная энергия (ЭПЭ) на единицу заряда. (Единица энергии — джоуль, а единица заряда — кулон.) Электрический потенциал показывает, какой будет электрическая потенциальная энергия заряженного объекта на каждый кулон заряда, который он имеет, или сколько джоулей энергии будет на один кулон. кулон. Единица измерения электрического потенциала, джоуль на кулон, названа вольт в память об Алессандро Вольта.Один вольт равен одному джоулю на кулон.
Хорошая аналогия — вода в мельничном пруду. Вода в пруду обладает потенциальной гравитационной энергией из-за того, насколько высоко она находится над уровнем моря. Когда вода падает, она теряет энергию. На холмах может быть пруд со 100 литрами воды и 1000 джоулей энергии в пруду, поэтому на литр приходится 10 джоулей энергии. В другом пруду может быть 100 литров воды, но при этом только 500 джоулей энергии, потому что пруд находится в более низкой долине.В этом пруду 5 джоулей на литр. Точно так же у нас может быть 100 кулонов заряда с 1000 джоулей электрической потенциальной энергии, хранящейся где-то, может быть, в электрической цепи. Электрический потенциал будет составлять 10 джоулей энергии на кулон. В другом месте, может быть, в другом месте той же электрической цепи, может быть электрический потенциал 5 джоулей на кулон.
Точно так же, как масса падает из места, где у нее более высокая потенциальная энергия, из самолета или другого места во Вселенной, на землю или другое место во Вселенной, где она имеет более низкую потенциальную энергию, то же самое происходит и с зарядами.Заряды всегда идут туда, где у них более низкий электрический потенциал или потенциал. Это движение также называется «падением». Группа зарядов или заряженный объект упадет с места с электрическим потенциалом 10 джоулей на кулон до места с электрическим потенциалом 5 джоулей на кулон или из места с электрическим потенциалом, равным 5 джоулей на кулон. электрический потенциал 10 вольт на единицу с электрическим потенциалом 5 вольт. Если на объекте есть 20 кулонов заряда, он упадет из-за наличия электрической потенциальной энергии (EPE) 200 джоулей (20 cx (10 Дж / c) = 200 джоулей) в месте с электрическим потенциалом 10 вольт до электрической потенциальной энергии 100 джоулей (20 cx (5 Дж / c) = 100 джоулей) в месте с электрическим потенциалом 5 вольт.
Хотя эта концепция также применима к гравитации, мы ее не используем. Почти всегда полезнее думать и использовать полную гравитационную потенциальную энергию, GPE, объекта, а не использовать GPE на килограмм. В электричестве очень часто более полезно использовать электрический потенциал, EPE на заряд, вместо того, чтобы использовать полную электрическую потенциальную энергию.
Электрический потенциал — это не то же самое, что электрическая потенциальная энергия. Это электрическая потенциальная энергия на единицу заряда.Электрический потенциал — это не то же самое, что разность электрических потенциалов. Разность электрических потенциалов также называется напряжением (см. Страницу напряжения).
Обратите внимание, что вольт и напряжение — это разные вещи. Вольт — это единица измерения, с помощью которой мы что-то измеряем. И электрический потенциал, и напряжение — это то, что мы измеряем, и вольт является единицей измерения для обоих. Да, немного сбивает с толку, но так оно и есть. Обозначение единицы вольт пишется через V (9 вольт или 9 В).Когда в формуле используется напряжение, символом для напряжения является строчная буква v (например, напряжение = ток x сопротивление или v = ir). Это отличает разницу между вольтами (V) и напряжением (v), когда имеется только однобуквенный символ. пройти мимо. Инженеры-электрики используют символ «e» для обозначения напряжения (например, e = ir), чтобы более четко различать разницу.
Что такое электрический потенциал? — Определение и формула — Видео и стенограмма урока
Что такое электрический потенциал?
Электрический потенциал — это «проталкивание» электричества через цепь.Электрический потенциал легко спутать с электрическим током, поэтому полезно думать об электрическом токе как о воде в душе, а электрический потенциал как о давлении воды. Как и давление воды, изменение напряжения может увеличивать или уменьшать поток электричества.
Если вы выключите душ, вода перестанет течь (ток больше не будет), но давление воды не изменится. Точно так же, как давление воды внезапно не станет лучше или хуже, когда вы снова включите душ, напряжение остается постоянным для каждого типа источника энергии.Батарея на 1,5 В остается 1,5 В независимо от того, используется она или нет.
Изменение электрического потенциала
Если продолжить аналогию: так же, как вы можете вызвать разнорабочего, чтобы помочь вам с проблемами давления воды, вы также можете увеличить или уменьшить напряжение. Заряженные частицы, крошечные части атомов, из которых когда-либо состоит все, мало что делают сами по себе, но если собрать вместе кучу заряженных частиц, у вас будет отличная вечеринка. Сборник заряда — это группа заряженных частиц, которые вместе в конечном итоге образуют достаточно потенциальной энергии, чтобы служить источником энергии.Ранее я сказал, что батарея — это электрохимический источник энергии, что является причудливым способом сказать, что она получает свой заряд за счет химической реакции, происходящей внутри батареи.
Плотность заряда , или плотность электронов в батарее, дает батарее ее напряжение. Если вы посмотрите на бытовую батарею D, такую как та, которую вы вставляете в фонарик, и небольшую батарею AAA, вроде той, которую вы вставляете в пульт дистанционного управления, вы увидите, что у них обоих есть напряжение 1.5 вольт. Это означает, что, несмотря на разницу в размерах, внутри них одинаковая плотность электронов или одинаковый электрический потенциал. Разница в размерах означает только то, что батарея большего размера D имеет большую мощность.
Чем плотнее сборник заряда, тем выше напряжение.Средний автомобильный аккумулятор составляет 12 вольт, что имеет смысл. Я хотел бы надеяться, что аккумулятор, питающий мою машину, имеет значительно больший импульс, чем аккумулятор, питающий мой пульт дистанционного управления.
Формула электрического потенциала
Чтобы вычислить электрический потенциал, мы должны начать с того, как мы измеряем работу. Работа рассчитывается умножением силы на расстояние. Для стрижки газона необходимо толкать газонокосилку на расстояние, поэтому вам нужно умножить силу, которую вы должны приложить для перемещения газонокосилки, на пройденное расстояние.Чем больше силы вы прикладываете или чем дальше толкаете газонокосилку, тем больше работы вы выполняете.
Мы измеряем работу в джоулей (Дж) , и если вы хотите почувствовать, сколько стоит работа в 1 джоуля, поднимите яблоко на один метр в воздух. Электрический заряд — это вторая половина формулы размышлений об электрическом потенциале. Заряд измеряется в кулонах (C) , по французскому физику Шарлю де Кулону.
Напряжение — это объем работы, который может быть выполнен за один заряд, и определяется делением работы на электрический заряд. Итак, простыми словами, один вольт эквивалентен одному джоулю на кулон. Поскольку «джоули на кулон» трудно повторять снова и снова, ученые придумали для обозначения вольт . Например, батарея D составляет 1,5 джоулей (работа) на кулон (заряд) или, проще говоря, 1,5 вольта.
Резюме урока
Электрический потенциал — это уровень мощности за потоком электричества, но его не следует путать с самим электрическим током.Мы часто называем электрический потенциал напряжением и измеряем его в вольтах (В) , что определяется делением работы (джоулей) на заряд (кулон). Чем больше напряжение, тем сильнее «толчок» электричества, действующий так же, как давление воды в душе.
Ключевые термины
- Вольтаическая куча : буквальная стопка из 24 медных и цинковых дисков, плюс картонные диски, пропитанные солью, дизайн Александра Вольта
- Аккумулятор : электрохимический источник энергии
- Вольт : единица измерения электрического потенциала
- Электрический потенциал : поток электроэнергии по цепи
- Сборник заряда : группа заряженных частиц
- Плотность заряда : плотность электронов в батарее, придает батарее напряжение
- Джоуля : измерение работы
- Кулоны : измерение заряда
Результаты обучения
Когда учащиеся закончат этот урок, они должны уметь:
- Определить электрический потенциал
- Определите, как определяется электрический потенциал
- Продемонстрируйте, как работают батареи
Электрический потенциал: определение, единицы и формула (с примерами)
Чтобы понять электричество, вы должны понимать электрическую силу и то, что произойдет с зарядами в присутствии электрического поля.Какие силы почувствует заряд? Как он в результате будет двигаться? Связанное с этим понятие — электрический потенциал, который становится особенно полезным, когда вы говорите о батареях и схемах.
Определение электрического потенциала
Вы можете вспомнить, что масса, помещенная в гравитационное поле, имеет определенное количество потенциальной энергии из-за своего местоположения. (Гравитационная потенциальная энергия составляет GMm / r , что уменьшается до мг / ч у поверхности Земли.) Точно так же заряд, помещенный в электрическое поле, будет иметь определенное количество потенциальной энергии из-за своего местоположения в поле.
Электрическая потенциальная энергия заряда q из-за электрического поля, создаваемого зарядом Q , определяется как:
PE_ {elec} = \ frac {kQq} {r}
Где r — расстояние между зарядами и константа Кулона k = 8,99 × 10 9 Нм 2 / C 2 .
Однако при работе с электричеством часто удобнее работать с величиной, называемой электрическим потенциалом (также называемым электростатическим потенциалом). Что такое электрический потенциал простыми словами? Ну, это электрическая потенциальная энергия на единицу заряда. Электрический потенциал V , тогда расстояние r от точечного заряда Q составляет:
V = \ frac {kQ} {r}
Где k — это та же кулоновская постоянная.
Единицей измерения электрического потенциала в системе СИ является вольт (В), где V = Дж / Кл (джоуль на кулон). По этой причине электрический потенциал часто называют «напряжением». Это устройство было названо в честь Алессандро Вольта, изобретателя первой электрической батареи.
Чтобы определить электрический потенциал в точке пространства в результате распределения нескольких зарядов, вы можете просто просуммировать электрические потенциалы каждого отдельного заряда. Обратите внимание, что электрический потенциал — это скалярная величина, поэтому это прямая сумма, а не векторная сумма.Однако, несмотря на то, что он является скаляром, электрический потенциал может принимать положительные и отрицательные значения.
Разность электрических потенциалов можно измерить с помощью вольтметра, подключив вольтметр параллельно к объекту, напряжение которого измеряется. (Примечание: электрический потенциал и разность потенциалов — это не совсем одно и то же. Первое относится к абсолютной величине в данной точке, а второе относится к разнице потенциалов между двумя точками.)
Эквипотенциальные поверхности и линии
Эквипотенциальные поверхности или линии — это области, вдоль которых электрический потенциал постоянен.Когда эквипотенциальные линии проводятся для данного электрического поля, они создают своего рода топографическую карту пространства, видимого заряженными частицами.
Эквипотенциальные линии действительно работают так же, как топографическая карта. Точно так же, как вы могли бы представить себе возможность определить, в каком направлении катится мяч, глядя на такую топографию, вы можете определить, в каком направлении будет двигаться заряд, по карте эквипотенциальности.
Думайте о регионах с высоким потенциалом как о вершинах холмов, а о регионах с низким потенциалом как о долинах.Подобно тому, как мяч катится вниз по склону, положительный заряд будет двигаться от высокого к низкому потенциалу. Точное направление этого движения, исключая любые другие силы, всегда будет перпендикулярно этим эквипотенциальным линиям.
Электрический потенциал и электрическое поле: Если вы помните, положительные заряды движутся в направлении линий электрического поля. Легко видеть, что силовые линии электрического поля всегда будут пересекать эквипотенциальные линии перпендикулярно.
Эквипотенциальные линии, окружающие точечный заряд, будут выглядеть следующим образом:
Обратите внимание, что они расположены ближе друг к другу рядом с зарядом.Это потому, что там потенциал падает быстрее. Если вы помните, соответствующие линии электрического поля для точки положительного точечного заряда направлены радиально наружу и, как и ожидалось, пересекают эти линии перпендикулярно.
Вот изображение эквипотенциальных линий диполя.
••• сделано с помощью приложения: https://phet.colorado.edu/sims/html/charges-and-fields/latest/charges-and-fields_en.html
Обратите внимание, что они антисимметричны: те, что рядом с положительный заряд — это значения с высоким потенциалом, а рядом с отрицательным зарядом — значения с низким потенциалом.Положительный заряд, размещенный где-нибудь поблизости, будет делать то, что вы ожидаете от катящегося под гору шарика: направляйтесь в «долину» с низким потенциалом. Однако отрицательные заряды действуют наоборот. Они «катятся в гору!»
Подобно тому, как потенциальная энергия гравитации преобразуется в кинетическую энергию для объектов, находящихся в свободном падении, так же электрическая потенциальная энергия преобразуется в кинетическую энергию для зарядов, свободно движущихся в электрическом поле. Таким образом, если заряд q пересекает потенциальную щель V, то величина его изменения в потенциальной энергии qV теперь равна кинетической энергии 1/2 мВ 2 .(Обратите внимание, что это также эквивалентно количеству работы, совершаемой электрической силой, чтобы переместить заряд на такое же расстояние. Это согласуется с теоремой о работе кинетической энергии.)
Батареи, ток и схемы
Вы, вероятно, знакомы с списками напряжений на аккумуляторах. Это показатель разности электрических потенциалов между двумя выводами батареи. Когда две клеммы соединены проводом, свободные электроны внутри проводника будут вынуждены двигаться.
Хотя электроны движутся от низкого потенциала к высокому, направление тока канонически определяется в противоположном направлении. Это потому, что оно было определено как направление потока положительного заряда до того, как физики узнали, что на самом деле физически движется электрон, отрицательно заряженная частица.
Однако, поскольку для большинства практических целей положительный электрический заряд, движущийся в одном направлении, выглядит так же, как отрицательный электрический заряд, движущийся в противоположном направлении, различие становится несущественным.
Электрическая цепь создается всякий раз, когда провод выходит из источника питания, такого как аккумулятор, с высоким потенциалом, затем подключается к различным элементам схемы (возможно, разветвляясь в процессе), затем возвращается вместе и снова подключается к клемме с низким потенциалом источник питания.
При таком подключении ток проходит по цепи, доставляя электрическую энергию различным элементам схемы, которые, в свою очередь, преобразуют эту энергию в тепло, свет или движение, в зависимости от их функции.
Электрическую цепь можно рассматривать как аналог труб с проточной водой. Батарея приподнимает один конец трубы, чтобы вода стекала вниз. У подножия холма батарея поднимает воду обратно в начало.
Напряжение аналогично тому, насколько высоко поднимается вода перед выпуском. Ток аналогичен потоку воды. И если на пути будут помещены различные препятствия (например, водяное колесо), это замедлит поток воды, поскольку энергия будет передаваться точно так же, как элементы контура.
Напряжение Холла
Направление положительного тока определяется как направление, в котором будет течь положительный свободный заряд при наличии приложенного потенциала. Это соглашение было принято до того, как вы узнали, какие заряды на самом деле движутся по цепи.
Теперь вы знаете, что, даже если вы определили, что ток идет в направлении потока положительного заряда, в действительности электроны текут в противоположном направлении. Но как определить разницу между положительными зарядами, движущимися вправо, и отрицательными зарядами, движущимися влево, если ток в любом случае одинаков?
Оказывается, движущиеся заряды испытывают силу в присутствии внешнего магнитного поля.
Для данного проводника в присутствии данного магнитного поля положительные заряды, движущиеся к правому концу, испытывают восходящую силу и, следовательно, будут собираться на верхнем конце проводника, создавая падение напряжения между верхним концом и нижний конец.
Электроны, движущиеся влево в том же магнитном поле, в конечном итоге также ощущают восходящую силу, и поэтому отрицательный заряд будет собираться на верхнем конце проводника. Этот эффект называется эффектом Холла .Измеряя, является ли напряжение Холла положительным или отрицательным, вы можете определить, какие частицы являются настоящими носителями заряда!
Примеры для изучения
Пример 1: Сфера имеет поверхность, равномерно заряженную 0,75 C. На каком расстоянии от ее центра находится потенциал 8 МВ (мегавольт)?
Чтобы решить, вы можете использовать уравнение для электрического потенциала точечного заряда и решить его для расстояния, r:
V = \ frac {kQ} {r} \ implies r = \ frac {kQ} {V}
Подстановка чисел дает окончательный результат:
r = \ frac {kQ} {V} = \ frac {(8.6} = 843 \ text {m}
Это довольно высокое напряжение даже на расстоянии почти километра от источника!
Пример 2: Электростатический распылитель краски имеет металлическую сферу диаметром 0,2 м с потенциалом 25 кВ (киловольт), которая отталкивает капли краски на заземленный объект. 3) (0.{-10} \ text {C}
Пример 3: В классическом ядерно-физическом эксперименте альфа-частица ускорялась в сторону ядра золота. Если энергия альфа-частицы составляла 5 МэВ (мегаэлектронвольт), насколько близко она могла подойти к ядру золота, прежде чем отклониться? (Альфа-частица имеет заряд +2 e , а ядро золота имеет заряд +79 e , где основной заряд e = 1,602 × 10 -19 C. )
Чтобы решить этот вопрос, вы используете соотношение между электрической потенциальной энергией и электрическим потенциалом, чтобы сначала решить для r:
PE_ {elec} = qV = q \ frac {kQ} {r} \ подразумевает r = q \ frac {kQ} {PE_ {elec}}
Затем вы начинаете вводить значения, очень осторожно относясь к единицам измерения.{-14} \ text {m}
Для сравнения, диаметр ядра золота составляет примерно 1,4 × 10 -14 м.
Учебник по физике: электрический потенциал
В предыдущем разделе Урока 1 было рассмотрено, что движение положительного тестового заряда в электрическом поле сопровождается изменениями потенциальной энергии. Гравитационная аналогия использовалась для объяснения причин взаимосвязи между местоположением и потенциальной энергией. Перемещение положительного пробного заряда против направления электрического поля похоже на перемещение массы вверх в пределах гравитационного поля Земли.Оба движения были бы подобны , идущему против природы , и потребовали бы работы внешней силы. Эта работа, в свою очередь, увеличит потенциальную энергию объекта. С другой стороны, движение положительного пробного заряда в направлении электрического поля будет похоже на падение массы в гравитационном поле Земли. Оба движения были бы подобны , идущему с природой , и происходили бы без необходимости работы внешней силы. Это движение приведет к потере потенциальной энергии.Потенциальная энергия — это запасенная энергия положения объекта, и она связана с расположением объекта в поле. В этом разделе Урока 1 мы представим концепцию электрического потенциала и свяжем это понятие с потенциальной энергией положительного тестового заряда в различных местах в пределах электрического поля.
Возвращение к гравитационной аналогииВокруг Земли существует гравитационное поле, которое оказывает гравитационное влияние на все массы, находящиеся в окружающем ее пространстве.Перемещение объекта вверх против гравитационного поля увеличивает его гравитационную потенциальную энергию. Объект, движущийся вниз в пределах гравитационного поля, потерял бы потенциальную гравитационную энергию. Когда гравитационная потенциальная энергия была введена в Блоке 5 Физического Класса, она была определена как энергия, запасенная в объекте из-за его вертикального положения над Землей. Количество гравитационной потенциальной энергии, хранящейся в объекте, зависело от количества массы, которым обладал объект, и величины высоты, на которую он был поднят.Гравитационная потенциальная энергия зависела от массы объекта и его высоты. У объекта с удвоенной массой будет вдвое больше потенциальной энергии, а у объекта с удвоенной высотой будет вдвое больше потенциальной энергии. Обычно высокие позиции называют локациями с высоким потенциалом энергии. Взгляд на диаграмму справа показывает ошибочность такого утверждения. Обратите внимание, что груз весом 1 кг, удерживаемый на высоте 2 метра, имеет такую же потенциальную энергию, как и масса весом 2 кг, удерживаемая на высоте 1 метр.Потенциальная энергия зависит не только от местоположения; это также зависит от массы. В этом смысле потенциальная гравитационная энергия зависит как минимум от двух типов величин:
1) Масса — свойство объекта, испытывающего гравитационное поле, и2) Высота — положение в пределах гравитационного поля
Таким образом, неправильно называть высокие позиции в гравитационном поле Земли позициями с высокой потенциальной энергией. Но есть ли какое-то количество, которое можно было бы использовать для оценки таких высот как имеющих большой потенциал обеспечения больших количеств потенциальной энергии массам, которые там находятся? Да! Хотя это не обсуждается во время блока по гравитационной потенциальной энергии, можно было бы ввести величину, известную как гравитационный потенциал — потенциальная энергия на килограмм.Гравитационный потенциал — это величина, которую можно использовать для оценки различных мест на поверхности Земли с точки зрения того, какой потенциальной энергией будет обладать каждый килограмм массы, когда он будет помещен туда. Величина гравитационного потенциала определяется как ПЭ / масса. Поскольку числитель и знаменатель PE / масса пропорциональны массе объекта, выражение становится независимым от массы. Гравитационный потенциал — это величина, зависящая от местоположения, которая не зависит от массы объекта, испытывающего поле.Гравитационный потенциал описывает эффекты гравитационного поля на объекты, которые находятся в различных местах внутри него.
Если гравитационный потенциал — это средство оценки различных мест внутри гравитационного поля с точки зрения количества потенциальной энергии на единицу массы, то концепция электрического потенциала должна иметь аналогичное значение. Рассмотрим электрическое поле, создаваемое положительно заряженным генератором Ван де Граафа. Направление электрического поля находится в том направлении, в котором будет проталкиваться положительный испытательный заряд; в этом случае направление направлено наружу от сферы Ван де Граафа.Потребуется работа, чтобы переместить положительный испытательный заряд к сфере против электрического поля. Количество силы, задействованной при выполнении работы, зависит от количества перемещаемого заряда (согласно закону электрической силы Кулона). Чем больше заряд на испытательном заряде, тем больше сила отталкивания и тем больше работы, которая должна быть проделана с ним, чтобы переместить его на такое же расстояние. Если два объекта с разным зарядом — один из которых в два раза больше заряда другого — перемещаются на одинаковое расстояние в электрическое поле, то объект с двойным зарядом потребует вдвое большей силы и, следовательно, в два раза больше работы.Эта работа изменит потенциальную энергию на величину, равную количеству проделанной работы. Таким образом, электрическая потенциальная энергия зависит от количества заряда на объекте, испытывающем поле, и от местоположения внутри поля. Так же, как и потенциальная гравитационная энергия, электрическая потенциальная энергия зависит как минимум от двух типов величин:
1) Электрический заряд — свойство объекта, испытывающего электрическое поле, и2) Расстояние от источника — местоположение в пределах электрического поля
В то время как электрическая потенциальная энергия зависит от заряда объекта, испытывающего электрическое поле, электрический потенциал зависит исключительно от местоположения.Электрический потенциал — это потенциальная энергия на заряд.
Понятие электрического потенциала используется для выражения эффекта электрического поля источника в терминах местоположения внутри электрического поля. Пробный заряд с удвоенным количеством заряда будет обладать удвоенной потенциальной энергией в данном месте; однако его электрический потенциал в этом месте будет таким же, как и у любого другого испытательного заряда. Положительный тестовый заряд будет иметь высокий электрический потенциал, когда он удерживается рядом с положительным зарядом источника, и с более низким электрическим потенциалом, когда он находится дальше.В этом смысле электрический потенциал становится просто свойством местоположения внутри электрического поля. Предположим, что электрический потенциал в данном месте составляет 12 джоулей на кулон, тогда это электрический потенциал заряженного объекта в 1 или 2 кулона. Утверждение, что электрический потенциал в данном месте составляет 12 джоулей на кулон, означало бы, что 2-кулоновский объект будет обладать 24 джоулями потенциальной энергии в этом месте, а объект 0,5 кулонов будет испытывать 6 джоулей потенциальной энергии в этом месте.
Электрический потенциал в цепяхКогда мы начнем обсуждать электрические схемы, мы заметим, что электрическая цепь с батарейным питанием имеет места с высоким и низким потенциалом. Заряд, движущийся по проводам цепи, будет сталкиваться с изменениями электрического потенциала при прохождении по цепи. В электрохимических элементах батареи между двумя выводами возникает электрическое поле, направленное от положительного вывода к отрицательному.Таким образом, перемещение положительного тестового заряда через ячейки от отрицательного вывода к положительному потребует работы, таким образом увеличивая потенциальную энергию каждого кулоновского заряда, который движется по этому пути. Это соответствует движению положительного заряда против электрического поля. По этой причине положительный вывод описывается как вывод с высоким потенциалом. Подобные рассуждения привели бы к заключению, что движение положительного заряда по проводам от положительного вывода к отрицательному будет происходить естественным образом.Такое движение положительного испытательного заряда должно происходить в направлении электрического поля и не требует работы. Заряд будет терять потенциальную энергию при движении по внешней цепи от положительного вывода к отрицательному. Отрицательная клемма описывается как клемма с низким потенциалом. Это назначение высокого и низкого потенциала клеммам электрохимической ячейки предполагает традиционное соглашение о том, что электрические поля основаны на направлении движения положительных тестовых зарядов.
В определенном смысле электрическая цепь — это не что иное, как система преобразования энергии. В электрохимических элементах электрической цепи с батарейным питанием химическая энергия используется для работы с положительным испытательным зарядом, чтобы переместить его с клеммы с низким потенциалом на клемму с высоким потенциалом. Химическая энергия преобразуется в электрическую потенциальную энергию во внутренней цепи (то есть в батарее). Попав на клемму с высоким потенциалом, положительный тестовый заряд будет перемещаться по внешней цепи и воздействовать на лампочку, двигатель или катушки нагревателя, преобразовывая свою электрическую потенциальную энергию в полезные формы, для которых схема была разработана.Положительный тестовый заряд возвращается к отрицательной клемме с низкой энергией и низким потенциалом, готовый к повторению цикла (или, лучше сказать, цепи , цепи ) снова и снова.
Проверьте свое понимание1. Величина электрического потенциала определяется как величина _____.
а. электрическая потенциальная энергияг. сила, действующая на заряд
г.потенциальная энергия на заряд
г. сила на заряд
2. Заполните следующую запись:
Когда над положительным испытательным зарядом выполняется работа с помощью внешней силы по перемещению его из одного места в другое, потенциальная энергия _________ (увеличивается, уменьшается) и электрический потенциал _________ (увеличивается, уменьшается).
3.На следующих диаграммах показано электрическое поле (представленное стрелками) и две точки, обозначенные A и B, расположенные внутри электрического поля. Положительный тестовый заряд показан в точке A. Для каждой диаграммы укажите, должна ли работа выполняться с зарядом, чтобы переместить его из точки A в точку B. Наконец, укажите точку (A или B) с наибольшей электрической потенциальной энергией и наибольший электрический потенциал.
Electric Potential — The Physics Hypertextbook
Обсуждение
введение
Вспомните историю развития электростатики.
- Начисления существуют.
- Заряды действуют друг на друга.
- Эта сила действует на расстояния любого размера.
У нас с вами нет проблем с этой последней идеей, но в свое время она называлась «действие на расстоянии» — довольно вежливо сформулированное оскорбление. Чтобы избежать концептуальных проблем, связанных с взаимодействием с бестелесной силой, Майкл Фарадей изобрел электрическое поле, и мир остался доволен.
Ну, какое-то время доволен.Затем кто-то указал, что электрическое поле является векторной величиной, и они вспомнили, что векторы громоздки и с ними трудно работать. Концептуальный комфорт был получен, но практическая реализация осталась неизменной. Будь прокляты эти ученые. Всегда ищу лучшее из всех возможных миров. Они хотели чего-то и концептуально удовлетворительного, и математически простого. Какая безрассудность!
Вы не поверите, но проблема уже была решена физиками и математиками, работающими над темами, не имеющими ничего общего с электричеством.Вода, ветер, тепло и растворенные вещества текут. Некоторые концептуальные и математические приемы, используемые для понимания этих предметов, также могут быть использованы для понимания электричества, а затем магнетизма и гравитации.
Что такое силовые линии, если не какая-то схема течения? Линии электрического поля «перетекают» от положительных зарядов к отрицательным. Положительный заряд — это как открытый кран, а отрицательный — как открытый сток. Любой, у кого есть рабочая раковина, может одним движением руки сделать грубую модель электрического диполя на кухне или в ванной.Подобные аналогии существуют для ветра, тепла и растворенных веществ. (Технически тепло и растворенные вещества диффундируют, а не текут, поэтому здесь аналогии немного слабее.)
Подумайте на мгновение о других вещах, которые текут, и подумайте о том, что заставляет их течь. Это будет ответ на нашу следующую концептуальную проблему. Создадим таблицу, в которой сравниваются похожие явления. Во всех случаях будет что-то, что течет, и что-то, что вызывает поток.
| поток… | обусловлено |
|---|---|
| речка (жидкая вода) | высота |
| ветер (атмосферные газы) | атмосферное давление |
| тепло (внутренняя энергия) | температура |
| растворенные вещества (растворенные вещества) | концентрация |
В каждом случае протекающая вещь может быть описана векторным полем (величина, имеющая величину и направление в любом месте), а вещь, которая вызывает поток, может быть описана разницей в скалярном поле (величина который имеет величину только в любом месте).
| поток… | вызвано разницей в… |
|---|---|
| векторное поле | скалярное поле |
Если мы сможем идентифицировать электрическое скалярное поле, которое вызывает электрическое векторное поле, мы упростили все электричество математически, поскольку скаляры математически проще векторов. «Определить», вероятно, не подходящее слово. «Define» больше нравится. Мы собираемся определить величину, которая играет ту же роль, что высота для рек, давление — для ветра, температура — для тепла, а концентрация — для растворенных веществ.
«Поток» электрического поля «вызван» разностью электрических потенциалов .
| поток… | вызвано разницей в… |
|---|---|
| электрическое поле (пробные заряды) | электрический потенциал |
Теперь вы должны спросить себя, что такое «электрический потенциал».
Во-первых, вторая половина термина «потенциал» не подразумевает, что у него есть возможность произойти или что-то, что может привести к полезности в будущем.Электрический потенциал места в космосе буквально не «может стать электрическим». Это неверное представление основано на другом значении слова «потенциал».
Настоящее значение слова «потенциал» в этом контексте сейчас неясно и, таким образом, является источником потенциальной путаницы. В контексте этого обсуждения потенциал означает нечто более близкое к тому, что дает силу, мощь, мощь или способность. Для физика существительное «потенциал» более тесно связано с прилагательными «мощный» или «потенция».В наши дни слово «потенциал» кажется скорее бессильным, чем мощным. «У меня есть power » — фраза, которая вдохновляет. «У меня есть потенциал , » — это фраза в поисках вдохновения.
Во-вторых, когда я написал термин «электрический потенциал», я не отрезал две трети пути от записи электрической потенциальной энергии. Это две отдельные (но связанные) концепции. Посмотрите, сможете ли вы следовать этой цепочке рассуждений. Обратите внимание, как я сказал «рассуждение», а не «логику». Это не доказательство.Математика покажет, как все взаимосвязано.
Разница в электрическом потенциале порождает электрическое поле. (Это концепция, которую я представляю вам в этой главе, которую вы читаете прямо сейчас.) Электрическое поле — это сила, приходящаяся на заряд, действующая на воображаемый пробный заряд в любом месте в космосе. (Эта концепция была представлена в главе перед этой.) Работа, проделанная путем помещения действительного заряда в электрическое поле, дает заряду электрическую потенциальную энергию. (Эта концепция называется теоремой работы-энергии и была введена очень давно, в одной далекой-далекой главе.) По переходному свойству (я полагаю) электрический потенциал порождает электрическую потенциальную энергию; и согласно рефлексивному свойству (другое предположение), электрический потенциал — это энергия на заряд, которую воображаемый пробный заряд имеет в любом месте в космосе.
Это слова. Нам нужна математика. Мы можем сделать это трудным путем (без исчисления) или простым способом (с исчислением). Твой выбор.
В любом случае, вот правила для символов, специфичных для этой темы…
- Символ электрического поля выделен жирным шрифтом в верхнем регистре E .Полужирно, потому что это векторная величина. Это прописные буквы из-за произвольного выбора. Это буква E, потому что это имеет смысл. Если вы видите символ, написанный курсивом с полосой в верхней части, например, E , это означает, что вы используете только среднее значение величины. Иногда этого достаточно.
- Обозначение электрической потенциальной энергии курсивом, прописными буквами U . Оно выделено курсивом, потому что это скалярная величина. Это прописные буквы, потому что… никто не знает.Это U, потому что вам нужно использовать какую-то букву. Думаю, теперь очередь за вами. Поскольку мы имеем дело с электрической потенциальной энергией, мы должны добавить нижний индекс в верхнем регистре E. Это дает нам U E . Если я забыл добавить подпись E, это потому, что вы должны знать из контекста, что это электрическая потенциальная энергия, а не что-то еще.
- Обозначение электрического потенциала выделено курсивом в верхнем регистре. V . Оно выделено курсивом, потому что это скалярная величина. Это заглавные буквы, чтобы соответствовать электрической потенциальной энергии (возможно).Это V, потому что V следует за U в алфавите… я думаю. Возможно, это также связано с названием единицы измерения электрического потенциала — вольт. Вы можете подумать, что я должен добавить к этому символу заглавную букву E с нижним индексом, например, V E , но я этого не сделаю. Никто не делает. Так редко обсуждают неэлектрические формы скалярного потенциала, что добавление нижнего индекса выполняется только для исключений — например, для гравитационного потенциала, V g .
без исчисления
Начнем с теоремы о работе-энергии.Когда работа закончена ( W ), энергия изменяется (∆ E ).
W = ∆ E
Более конкретно, когда работа выполняется против электрической силы ( F E ), электрическая потенциальная энергия изменяется (∆ U E ). Напомним, что работа — это сила, умноженная на смещение ( d ). Над символом силы есть полоса, указывающая, что мы будем использовать среднее значение. Это одно из ограничений выводов без исчисления.
F E d = ∆ U E
Разделите обе стороны по заряду ( q ).
Немного переставить.
Отношение силы к заряду слева называется , электрическое поле ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Единственное, что изменилось, это то, что сейчас мы имеем дело со средними значениями. Отношение энергии к заряду справа называется , электрический потенциал ( В, ).Это новая идея, которая сейчас обсуждается в этой книге.
Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в космосе. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для каждого места в космосе. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.
Электрическое поле и электрический потенциал связаны смещением.Временное смещение поля потенциальное…
Ed = ∆ V
или поле является потенциально избыточным смещением, если хотите.
На языке причудливых математических вычислений поле — это градиент потенциала, потому что реальный мир причудлив, я имею в виду трехмерный. Градиент — это трехмерный эквивалент наклона. Обычный уклон одномерный, потому что линия одномерная (даже если она не прямая). При движении по кривой нужно принимать только одно решение.Мне идти вперед или вернуться? В обычном евклидовом пространстве у нас есть три варианта. Вверх или вниз? Влево или вправо? Вперед или назад?
исчисление
Начнем с теоремы о работе-энергии. Когда работа закончена ( W ), энергия изменяется (∆ E ).
W = ∆ E
Более конкретно, когда работа выполняется против электрической силы ( F E ), электрическая потенциальная энергия изменяется (∆ U E ).Напомним, что работа — это интеграл сила-перемещение.
| – | ⌠ ⌡ | F E · d r = ∆ U E |
Разделите обе стороны по заряду ( q ).
| – | 1 | ⌠ ⌡ | F E · d r = | 1 | ∆ U E |
| q | q |
Немного переставить.
| – | ⌠ ⌡ | Ф E | · d r = | ∆ U E |
| q | q |
Отношение силы к заряду слева называется , электрическое поле ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Отношение энергии к заряду справа называется , электрический потенциал ( В, ).Это новая идея, которая сейчас обсуждается в этой книге.
Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в космосе. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для каждого места в космосе. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.
Электрическое поле и электрический потенциал связаны интегралом по путям, который работает для всех видов ситуаций.Мой совет при работе с интегралом по путям — всегда выбирать самый простой путь для работы. Электричество — это консервативная сила, поэтому выполняемая им работа не зависит от выбранного пути. Это уравнение говорит о более поразительном. Интеграл слева настолько независим от пути, что его значение зависит только от электрического потенциала в начале и в конце пути. Если вам удастся найти эти два числа и вычесть их, вы сделали интеграл целиком. Если бы таким образом работало больше интегралов, студенты не зацикливались бы на исчислении.
| – | ⌠ ⌡ | E · d r = ∆ V |
Электрическое поле и электрический потенциал также связаны производной, которая работает только для одномерных ситуаций — ситуаций со сферической, цилиндрической или плоской симметрией.
| E = — | д | V r̂ |
| др |
В более изящных терминах математики поле — это градиент потенциала, потому что реальный мир более интересен, чем одномерная задача.Градиент является эквивалентом производной в более высоких измерениях (в этой книге — двух и трех измерениях). Это соотношение работает для всех видов симметрии и несимметрии.
E = −∇ V
Греческая буква дельта выглядит как треугольник, направленный вверх (∆). Перевернутая дельта называется дель (∇). Символы дельта и дель являются примерами математических устройств, называемых операторами , — символами, указывающими на необходимость выполнения операции над переменной.Дельта-оператор неоднократно обсуждался в этой книге. Оператор del немного реже.
Оператор дельты используется всякий раз, когда требуется изменение или разность количества. Вернемся немного назад к уравнению, которое связывает электрическое поле с электрическим потенциалом через интеграл по путям.
| – | ⌠ ⌡ | E · d r = ∆ V |
Здесь ∆ V означает разность электрического потенциала между двумя точками — обычно начальным или начальным положением (обозначено в этой книге с нижним индексом ноль) и конечным или конечным положением (указанным в этой книге без подстрочного индекса). .
| р | ||
| – | ⌠ ⌡ | E · d r = V — V 0 |
| r 0 |
В декартовых координатах оператор del представляет собой сумму частных производных в трех направлениях единичного вектора. (В некартовых координатах del немного сложнее).
| ∇ = î | ∂ | + ĵ | ∂ | + кО | ∂ |
| ∂ x | ∂ y | ∂ z |
Когда оператор del применяется к скалярному полю, результирующая операция известна как градиент . Вернитесь немного назад. Уравнение, которое говорит, что электрическое поле — это градиент электрического потенциала…
E = −∇ V
выглядит так при раскрытии оператора del…
| E = — î | ∂ | В — ĵ | ∂ | V — k̂ | ∂ | В |
| ∂ x | ∂ y | ∂ z |
и тому подобное, когда члены переставлены так, что скаляры предшествуют векторам…
| E = — | ∂ | В или — | ∂ | В ĵ — | ∂ | V k̂ |
| ∂ x | ∂ y | ∂ z |
Может быть, теперь вы понимаете, почему был изобретен символ дель.В компактном уравнении 5 символов (не считая пробелов). В расширенном уравнении 23 (с учетом «шляп», но без учета пробелов).
Подождите. Что за дело со всеми этими минусами? Позвольте мне объяснить… позже.
шт.
электрический потенциал
Что нового в этой главе этой книги? Все понятие электрического потенциала. Я представил электрический потенциал как способ решить проблемы векторной природы электрического поля, но электрический потенциал — это концепция, которая имеет право на существование сама по себе.Электрический потенциал — это электрическая потенциальная энергия тестового заряда, деленная на заряд этого тестового заряда.
Старые вещи. SI — это сокращение от le Système international d’unités на французском языке или International System of Units на английском языке. Единица измерения энергии в системе СИ — джоуль, названная в честь Джеймса Джоуля, английского пивовара, ставшего физиком, который определил, что тепло и электричество являются формами энергии, эквивалентными другим формам механической энергии, таким как гравитационная потенциальная энергия и кинетическая энергия.Единицей заряда в системе СИ является кулон, названный в честь Шарля-Огюстена Кулона, французского дворянина и солдата, ставшего физиком, открывшего правило обратных квадратов электростатической силы. Единица смещения (или расстояния) в системе СИ — это метр — слово, названное в честь никого и в конечном итоге образованное от греческого слова, обозначающего меру (μετρον, metron ).
Новинка. Единица измерения электрического потенциала в системе СИ — вольт, названная в честь итальянского дворянина, ставшего физиком Алессандро Вольта, полное имя которого — удивительно длинный граф Алессандро Джузеппе Антонио Анастасио Вольта.Сегодняшняя шутка состоит в том, что полное имя Вольты было настолько длинным, что, когда они сократили его до названия подразделения, они зашли слишком далеко и отрезали последнюю букву «а». Единицей электрического потенциала по праву следует называть вольта, а не вольт (шутка, которую ценят только педантичные из нас). Граф Вольта больше всего известен как изобретатель электрохимической ячейки — того, что мы теперь ошибочно называем батареей (еще одно отличие, которое ценится только педантиками — батарея — это совокупность электрохимических ячеек).Для тех, кто заботится о важных вещах, вольт — это джоуль на кулон.
[V = J / C]
Разность электрических потенциалов между двумя точками равна одному вольт, если для перемещения одного кулона заряда из одного места в другое требуется один джоуль работы.
электрическое поле
Электрический потенциал — это способ объяснить «сложное» векторное поле в терминах «легкого» скалярного поля. По определению, электрическое поле — это сила, приходящаяся на заряд воображаемого пробного заряда.
Посредством длинного объяснения, электрическое поле — это также градиент электрического потенциала (скорость изменения электрического потенциала со смещением).
Установите две величины равными…
, а затем установите их единицы равными.
[N / C = В / м]
Ньютон на кулон и вольт на метр являются эквивалентными единицами измерения электрического поля. Вольт на метр чаще используют те, кто действительно измеряет вещи, потому что вольт (который можно измерить с помощью вольтметра) и измеритель (который можно измерить линейкой любого размера, включая метрическую палочку с соответствующим названием) намного больше. легче измерить, чем силу (которую, я полагаю, можно измерить с помощью пружинной шкалы или тензодатчика, прикрепленного к заряженному объекту) и заряд (который можно измерить с помощью какого-либо известного мне устройства).
электрическая потенциальная энергия
Если вольт — это джоуль на кулон, то джоуль — это кулон-вольт. Когда один кулон заряда перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один джоуль.
[J = CV]
Для некоторых приложений джоуль слишком велик, в основном потому, что кулон слишком велик. Обычная малая единица заряда — элементарный заряд [е]. Это самый маленький заряд, который когда-либо наблюдался. Некоторые частицы, такие как протон, имеют этот заряд со знаком плюс ( q протон = +1 e), а некоторые, как электрон, имеют его со знаком минус ( q электрон = −1 e ).Когда один элементарный заряд перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один электронвольт [эВ] — плюс или минус один электронвольт в зависимости от знака заряда и знака разности потенциалов. Электронвольт используется для некоторых приложений в электромагнетизме; твердое тело, атомная физика, ядерная физика и физика элементарных частиц; и смежные науки, такие как биофизика, химия и астрономия. Это хороший маленький блок для небольших физических систем, таких как атомы и молекулы.На самом деле это слишком мало для ядерной физики и физики элементарных частиц, но следующей по величине единицей СИ является джоуль, который на 19 порядков больше.
| qV = | qV |
| 1 электронвольт = | (1 элементарный заряд) (1 вольт) |
| 1 электронвольт = | (1,6 × 10 −19 кулонов) (1 вольт) |
| 1 электронвольт = | 1,6 × 10 −19 джоулей |
| 1 эВ = | 1.6 × 10 −19 Дж |
Электронвольт на самом деле не является единицей СИ, поскольку элементарный заряд не определяется как единица измерения. Заряд электрона, протона или чего-либо еще с элементарным зарядом должен быть получен экспериментально и поэтому является неопределенным. Электронвольт был «принят для использования» с SI CIPM ( le Comité international des poids et mesures или Международный комитет мер и весов).
эксперимент милликена
Роберт Милликен (1865–1953) США
аппарат
выводов
Обзор | Безграничная физика
Связь между электрическим потенциалом и полем
Электрический потенциал и поле связаны между собой в том смысле, что потенциал — это свойство поля, которое описывает действие поля.
Цели обучения
Объясните взаимосвязь между электрическим потенциалом и электрическим полем
Основные выводы
Ключевые моменты
- Электрическое поле — мера силы на единицу заряда; электрический потенциал — это мера энергии на единицу заряда.
- Для однородного поля соотношение между электрическим полем (E), разностью потенциалов между точками A и B (Δ) и расстоянием между точками A и B (d) составляет: [latex] \ text {E} = — \ frac {\ Delta \ phi} {\ text {d}} [/ latex] Если поле неоднородно, для решения требуется исчисление.
- Потенциал — это свойство поля, которое описывает действие поля на объект.
Ключевые термины
- электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
- электрический потенциал : потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.
Связь между электрическим потенциалом и полем аналогична взаимосвязи между гравитационным потенциалом и полем в том смысле, что потенциал — это свойство поля, описывающее действие поля на объект (см.).
Электрическое поле и потенциал в одном измерении : Наличие электрического поля вокруг статического точечного заряда (большая красная точка) создает разность потенциалов, в результате чего тестовый заряд (маленькая красная точка) испытывает силу и перемещается.
Электрическое поле похоже на любое другое векторное поле — оно создает силу, основанную на стимуле, и имеет единицы силы, умноженные на обратный стимул. В случае электрического поля стимулом является заряд, и, следовательно, единицы — NC -1 .Другими словами, электрическое поле — это мера силы на единицу заряда.
Электрический потенциал в точке — это отношение потенциальной энергии любой заряженной частицы в этой точке к заряду этой частицы. Его единицы: JC -1 . Таким образом, электрический потенциал — это мера энергии на единицу заряда.
В единицах измерения электрический потенциал и заряд тесно связаны. У них общий коэффициент обратных кулонов (C -1 ), в то время как сила и энергия различаются только на коэффициент расстояния (энергия — это произведение силы на расстояние).
Таким образом, для однородного поля соотношение между электрическим полем (E), разностью потенциалов между точками A и B (Δ) и расстоянием между точками A и B (d) составляет:
[латекс] \ text {E} = — \ frac {\ Delta \ phi} {\ text {d}} [/ latex].
Коэффициент -1 возникает из-за отталкивания положительных зарядов: положительный заряд будет отталкиваться от положительно заряженной пластины в сторону места с более высоким напряжением.
Приведенное выше уравнение представляет собой алгебраическое соотношение для однородного поля.В более чистом смысле, без предположения об однородности поля, электрическое поле — это градиент электрического потенциала в направлении x:
[латекс] \ text {E} _ \ text {x} = — \ frac {\ text {dV}} {\ text {dx}} [/ latex].
Это можно вывести из основных принципов. Учитывая, что ∆P = W (изменение энергии заряда равно работе, выполненной над этим зарядом), применяя закон сохранения энергии, мы можем заменить ∆P и W другими членами. ∆P может быть заменен на его определение как произведение заряда (q) и дифференциала потенциала (dV).Затем мы можем заменить W на его определение как произведение q, электрического поля (E) и разницы расстояний в направлении x (dx):
[латекс] \ text {qdV} = — \ text {qE} _ \ text {xdx} [/ latex].
Разделив обе части уравнения на q, получим предыдущее уравнение.
Электрическая потенциальная энергия и разность потенциалов
Электрическая потенциальная энергия возникает в результате сил между зарядами; разность потенциалов — это энергия, необходимая для перемещения заряда из точки A в точку B.
Цели обучения
Вычислить потенциальную энергию между зарядами
Основные выводы
Ключевые моменты
- Электрическая потенциальная энергия — это тип потенциальной энергии, возникающей в результате действия кулоновских сил. Потенциальная энергия (UE) между зарядами q и Q может быть вычислена как функция расстояния между зарядами (r): [latex] \ text {U} _ \ text {E} (\ text {r}) = \ frac {\ text {qQ}} {4 \ pi \ epsilon_0 \ text {r}} [/ latex].
- Формула для потенциальной энергии может быть изменена для потенциала между многими зарядами, если учитываются взаимодействия каждого заряда с каждым другим зарядом в системе.Например, потенциал между тремя зарядами можно определить с помощью следующей формулы: [latex] \ text {U} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0 \ text {r}} (\ frac {\ text {Q} _1 \ text {Q} _2} {\ text {r} {12}} + \ frac {\ text {Q} _2 \ text {Q} _3} {\ text {r} {23} } + \ frac {\ text {Q} _1 \ text {Q} _3} {\ text {r} {13}}) [/ latex].
- Разность потенциалов или напряжение — это разница в электрической потенциальной энергии между двумя точками. Он обозначается ∆V и измеряется в вольтах или джоулях на кулон.
Ключевые термины
- кулон : В Международной системе единиц производная единица электрического заряда; количество электрического заряда, переносимого током в 1 ампер, протекающим в течение 1 секунды.Символ: C
- потенциальная энергия : энергия, которой обладает объект из-за его положения (в гравитационном или электрическом поле) или его состояния (в виде растянутой или сжатой пружины, в качестве химического реагента или за счет наличия массы покоя)
Электрическая потенциальная энергия — это тип потенциальной энергии, возникающей в результате кулоновских сил. Он измеряется в джоулях и зависит от расположения заряженных частиц относительно друг друга, а также от величины их соответствующих зарядов.
Потенциальная энергия (U E ) между зарядами q и Q может быть рассчитана как функция расстояния между зарядами (r):
[латекс] \ text {U} _ \ text {E} (\ text {r}) = \ frac {\ text {qQ}} {4 \ pi \ epsilon_0 \ text {r}} [/ latex]
Если есть три или более зарядов, приведенная выше формула может быть изменена так, чтобы потенциальные энергии между всеми зарядами суммировались. Рассмотрим, например, случай с обвинениями Q 1 , Q 2 и Q 3 :
[латекс] \ text {U} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0 \ text {r}} (\ frac {\ text {Q} _1 \ text {Q} _2} {\ text {r} {12}} + \ frac {\ text {Q} _2 \ text {Q} _3} {\ text {r} {23}} + \ frac {\ text {Q} _1 \ text { Q} _3} {\ text {r} {13}}) [/ latex]
В этом примере r 12 представляет расстояние между Q 1 и Q 2 , r 23 представляет расстояние между Q 2 и Q 3 , а r 13 представляет расстояние между Q 1 и Q 3 .Приведенная выше формула может быть изменена для любого количества зарядов.
Возможная разница
Разность потенциалов или напряжение — это разница в электрической потенциальной энергии между двумя точками. Он обозначается ∆V и измеряется в вольтах или джоулях на кулон.
Разность электрических потенциалов : Краткий обзор разности электрических потенциалов и электрической потенциальной энергии для начинающих студентов-физиков.
Напряжение — это работа на единицу заряда, которую необходимо совершить против статического электрического поля, чтобы переместить заряд из одной точки в другую.Он может представлять собой источник энергии или потерянную, накопленную или использованную энергию. Напряжение также определяется таким образом, что отрицательные заряды тянутся к более высоким напряжениям, а положительные заряды перемещаются к более низким напряжениям. Таким образом, ток в проводах течет от более высокого напряжения к более низкому.
Разница потенциалов не зависит от пути, пройденного от одной точки до другой, и может быть измерена любым из множества инструментов. К ним относятся вольтметр, потенциометр и осциллограф. Чаще всего его измеряют в схемах, и в таких ситуациях его можно вычислить с помощью закона Ома, который будет рассмотрен в более позднем атоме.
Разность потенциалов в статическом поле : Когда заряд q перемещается из точки A в точку B, разность потенциалов не зависит от пройденного пути.
Электрическое поле и изменение электрического потенциала
Электрическое поле — это градиент потенциала, который обратно пропорционален расстоянию от точки интереса до заряда.
Цели обучения
Вычислить электрический потенциал, создаваемый распределением заряда постоянного значения
Основные выводы
Ключевые моменты
- Для любого заряда постоянной величины (Q) потенциал (VE) на определенном расстоянии от него (r) можно рассчитать по формуле: [latex] \ text {V} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0} \ frac {\ text {Q}} {\ text {r}} [/ latex] Где ε0 — электрическая постоянная, также известная как диэлектрическая проницаемость свободного пространства.
- Для одного точечного заряда потенциал будет постоянным для всех точек на определенном радиальном расстоянии. Несколько точек с одинаковым потенциалом известны как эквипотенциальные.
- Когда несколько зарядов создают поле, эквипотенциальные линии приобретают неправильную форму. Это связано с тем, что поля, создаваемые каждым зарядом, перекрываются, таким образом, потенциал увеличивается в любой точке по сравнению с тем, который возник бы от одного или другого заряда.
Ключевые термины
- эквипотенциальный : область, каждая точка которой имеет одинаковый потенциал.
- радиальный : перемещение по радиусу.
Любой заряд создает вокруг себя векторное поле (известное как электрическое поле). Электрическое поле — это градиент потенциала, который обратно пропорционален расстоянию от интересующей точки до заряда. Размещение второго заряда в системе («пробный заряд») приводит к тому, что два заряда испытывают силу (единицы поля — ньютоны, мера силы на кулон), заставляя заряды перемещаться относительно друг друга.Проще всего смоделировать взаимодействия между двумя зарядами так, чтобы один считался неподвижным, пока пробный заряд движется.
По мере движения пробного заряда потенциал между ним и другим зарядом изменяется, как и электрическое поле. Связь между потенциалом и полем (E) является дифференциальной: электрическое поле — это градиент потенциала (V) в направлении x. Это может быть представлено как:
[латекс] \ text {E} _ \ text {x} = — \ frac {\ text {dV}} {\ text {dx}} [/ latex].
Эквипотенциальные линии : Изолированный точечный заряд Q с его линиями электрического поля (синий) и эквипотенциальными линиями (зеленый)
Таким образом, когда тестовый заряд перемещается в направлении x, скорость его изменения потенциала является величиной электрического поля.
В момент перед движением пробного заряда его потенциальная энергия максимальна, а его кинетическая энергия равна 0. Для любого заряда постоянной величины (Q) потенциал на определенном расстоянии от него (r) может быть рассчитан из следующее уравнение:
[латекс] \ text {V} _ \ text {E} = \ frac {1} {4 \ pi \ epsilon_0} \ frac {\ text {Q}} {\ text {r}} [/ latex],
, где ε 0 — электрическая постоянная, также известная как диэлектрическая проницаемость свободного пространства. Движение к заряду и от него приводит к изменению потенциала; соотношение между расстоянием и потенциалом обратное.
Для одного точечного заряда потенциал будет постоянным для всех точек на определенном радиальном расстоянии. Несколько точек с одинаковым потенциалом известны как эквипотенциальные. В случае полей, созданных одиночным точечным зарядом, все точки на любом круге с центром вокруг точечного заряда будут эквипотенциальными, как показано на.
показывает, что когда несколько зарядов создают поле, эквипотенциальные линии приобретают неправильную форму. Это связано с тем, что поля, создаваемые каждым зарядом, перекрываются, таким образом, потенциал увеличивается в любой точке по сравнению с тем, который возник бы от одного или другого заряда.
Потенциалы и заряженные проводники
Электрический потенциал внутри заряженного проводника равен нулю, но может быть вычислен как ненулевое значение вне заряженного проводника.
Цели обучения
Определить электрический потенциал внутри и снаружи заряженного проводника
Основные выводы
Ключевые моменты
- Электрический потенциал (∆V) и поле (E) связаны согласно интегралу: [latex] \ Delta \ text {V} = — \ int _ {\ text {i}} ^ {\ text {f}} \ ! \ vec {\ text {E}} \ cdot \ mathrm {\ text {d}} \ vec {\ text {l}} [/ latex], где l — расстояние между двумя точками, между которыми определяется разность потенциалов.
- Учитывая, что электрическое поле постоянно равно 0 для любого места внутри заряженного проводника, разность потенциалов в том же объеме не может иметь никакого значения, кроме 0.
- Для точек вне проводника потенциал отличен от нуля и может быть рассчитан в зависимости от поля и расстояния от проводника.
Ключевые термины
- электрический потенциал : потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.
- электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
- работа : мера энергии, затрачиваемой на перемещение объекта; чаще всего, сила, умноженная на смещение. Если объект не двигается, работа не выполняется.
Когда проводник становится заряженным, этот заряд распространяется по его поверхности, пока не будет достигнуто электростатическое равновесие. Его поверхность эквипотенциальная.
Все точки внутри заряженного проводника испытывают электрическое поле равным 0. Это происходит потому, что силовые линии от зарядов на поверхности проводника одинаково противостоят друг другу. Однако, имея электрическое поле, равное нулю во всех точках внутри проводника, электрический потенциал внутри проводника не обязательно равен нулю для всех точек внутри того же проводника. Это можно доказать, связав электрическое поле и потенциал.
Электрический заряд на острой точке проводника : Силы отталкивания, направленные к более изогнутой поверхности справа, направлены больше наружу, чем вдоль поверхности проводника.\ text {f} \! \ vec {\ text {E}} \ cdot \ mathrm {\ text {d}} \ vec {\ text {l}} [/ latex]
Наконец, мы выводим уравнение:
[латекс] \ text {dV} = — \ vec {\ text {E}} \ cdot \ mathrm {\ text {d}} \ vec {\ text {l}} = 0 [/ латекс]
Таким образом, мы можем заключить, что, учитывая, что электрическое поле постоянно равно 0 для любого места внутри заряженного проводника, разность потенциалов в том же объеме должна быть постоянной и равной 0.
С другой стороны, для точек вне проводника потенциал отличен от нуля и может быть определен тем же самым уравнением в зависимости от поля и расстояния от проводника.
Равномерное электрическое поле
Электрическое поле, которое является однородным, — это такое поле, которое достигает недостижимой стабильности, будучи постоянным повсюду.
Цели обучения
Описание свойств и приближения однородного электрического поля
Основные выводы
Ключевые моменты
- Однородное электрическое поле — это приближение, позволяющее выполнять простые вычисления, не требующие дифференциального исчисления. Каждое поле будет иметь по крайней мере некоторую неровность, хотя некоторые могут быть почти однородными.
- Уравнение для величины однородного электрического поля: [latex] \ text {E} = \ frac {- \ Delta \ phi} {\ text {d}} [/ latex], где E — поле, Δ — разность потенциалов между пластинами, а d — расстояние между пластинами.
- Для случая, когда положительный заряд q перемещается из точки A с определенным потенциалом (V 1 ) в точку B с другим потенциалом (V 2 ), это уравнение выглядит следующим образом: [латекс] \ text { W} = — \ text {q} (\ text {V} _2- \ text {V} _1) [/ latex] Разница (V 2 -V 1 ) также может быть представлена как ∆V или V АБ .
- В однородных полях также просто вычислить разность потенциалов: [latex] \ text {V} _ {\ text {AB}} = \ text {Ed} [/ latex] В этом случае напряженность поля E, а расстояние между точками A и B находится d.
Ключевые термины
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
- электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
Однородное поле — это то, в котором электрическое поле постоянно на всем протяжении. Как и так называемая «поверхность без трения» в механике, однородное поле является идеальной, но нереальной ситуацией, которая упрощает вычисления. Уравнения с неоднородными электрическими полями требуют использования дифференциального исчисления.
Однородность электрического поля можно приблизить, поместив две проводящие пластины параллельно друг другу и создав между ними разность потенциалов.В таком случае поле возле его краев будет немного изменяться, но оно будет примерно постоянным во всех остальных областях.
Уравнение для величины однородного электрического поля:
[латекс] \ text {E} = \ frac {- \ Delta \ phi} {\ text {d}} [/ latex]
где E — поле, Δ — разность потенциалов между пластинами, а d — расстояние между пластинами. Коэффициент -1 возникает из-за того, что положительные заряды отталкиваются, и, таким образом, положительный заряд будет отталкиваться от положительной пластины в направлении, противоположном направлению увеличения напряжения.
Однородность электрического поля позволяет легко рассчитать работу, выполняемую при перемещении испытательного заряда. Для случая, когда положительный заряд q перемещается из точки A с определенным потенциалом (V 1 ) в точку B с другим потенциалом (V 2 ), это уравнение имеет вид:
[латекс] \ text {W} = — \ text {q} (\ text {V} _2- \ text {V} _1) [/ латекс]
Разница (V 2 -V 1 ) также может быть представлена как ∆V или V AB .В однородных полях также просто связать ∆V с напряженностью поля и расстоянием (d) между точками A и B:
[латекс] \ text {V} _ {\ text {AB}} = \ text {Ed} [/ latex]
Взаимосвязи в однородном электрическом поле : На этом изображении работа (W), напряженность поля (E) и разность потенциалов (∆V) определены для точек A и B в рамках построения однородного потенциального поля между положительными и отрицательные пластины.
Энергосбережение
Энергия сохраняется при движении заряженной частицы через электрическое поле, как и в любой другой физической ситуации.
Цели обучения
Сформулировать принцип сохранения энергии заряженной частицы в электрическом поле
Основные выводы
Ключевые моменты
- При наличии стационарного испытательного заряда в определенном месте приложенное электрическое поле заставит заряд переместиться в один или другой конец, в зависимости от заряда.
- Положительные тестовые заряды будут двигаться в направлении поля; отрицательные заряды будут двигаться в противоположном направлении.
- В момент приложения поля неподвижный пробный заряд имеет нулевую кинетическую энергию, а его электрическая потенциальная энергия максимальна.Затем заряд ускоряется, и его кинетическая энергия (от движения) увеличивается по мере уменьшения его потенциальной энергии. Сумма энергий всегда постоянна.
- Формулу, иллюстрирующую сохранение энергии, можно записать разными способами, но все выражения основаны на простой предпосылке приравнивания начальной и конечной сумм кинетической и потенциальной энергии.
Ключевые термины
- кинетическая энергия : энергия, которой обладает объект из-за его движения, равная половине массы тела, умноженной на квадрат его скорости.
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
- потенциальная энергия : энергия, которой обладает объект из-за его положения (в гравитационном или электрическом поле) или его состояния (в виде растянутой или сжатой пружины, в качестве химического реагента или за счет наличия массы покоя)
Энергия сохраняется при движении заряженной частицы через электрическое поле, как и в любой другой физической ситуации.Это явление можно выразить как равенство суммарной кинетической ( E кинет ) и электрической потенциальной ( E el ) энергий:
[латекс] (\ text {E} _ {\ text {kin}} + \ text {E} _ {\ text {el}}) _ {\ text {initial}} = (\ text {E} _ { \ text {kin}} + \ text {E} _ {\ text {el}}) _ {\ text {final}} [/ latex]
При стационарном испытательном заряде в определенном месте приложенное электрическое поле заставит заряд переместиться в один или другой конец, в зависимости от заряда (положительные испытательные заряды будут двигаться в направлении поля; отрицательные заряды будут двигаться внутрь). 2 + \ text {U}) _ {\ text {final}} [/ latex]
, где m и v — масса и скорость электрона, соответственно, а U — электрическая потенциальная энергия. U можно рассчитать следующим образом:
[латекс] \ text {U} = \ text {q} _0 \ text {V} = \ text {k} \ frac {\ text {q} _0 \ text {q}} {\ text {r}} [ / латекс]
, где V — разность потенциалов, k — постоянная, q 0 — пробный заряд, q — другой заряд, а r — расстояние между зарядами.
Члены формулы сохранения энергии можно переписать разными способами, но все выражения основаны на простой посылке приравнивания начальной и конечной сумм кинетической и потенциальной энергии.
Сходства между действием гравитационного и электрического полей на объекте : Заряд + q перемещается вниз по электрическому полю так же, как объект m перемещается вниз по холму. В обоих случаях движущаяся частица переходит из состояния с более высокой потенциальной энергией в состояние с более низкой потенциальной энергией.
Электрон-вольт
Электрон-вольт — единица энергии, используемая в физике элементарных зарядов и электричества.
Цели обучения
Преобразование электрон-вольт в единицы энергии СИ
Основные выводы
Ключевые моменты
- Электрон-вольт определяется как количество энергии, полученной или потерянной зарядом электрона, перемещающегося через разность электрических потенциалов в один вольт.Его значение примерно равно 1,602 × 10 -19 Дж. .
- Электрон-вольт стал полезным благодаря экспериментам. Ученые, работающие с электростатическими ускорителями частиц, обычно использовали в своей работе соотношение между энергией (E), зарядом (q) и разностью потенциалов (V). Это соотношение: E = qV.
- В качестве энергии электрон-вольт можно использовать во многих вычислениях, включая импульс, массу, длину волны и температуру.
Ключевые термины
- разность потенциалов : разница в потенциальной энергии между двумя точками в электрическом поле; разница в заряде между двумя точками в электрической цепи; Напряжение.
- ускоритель частиц : Устройство, которое ускоряет электрически заряженные частицы до чрезвычайно высоких скоростей с целью инициирования высокоэнергетических реакций или получения высокоэнергетического излучения.
- электрон-вольт : Устройство для измерения энергии субатомных частиц; энергия равна энергии, полученной электроном, движущимся через разность потенциалов в один вольт. Эквивалентно 1,6022 x 10-19 джоулей.
Обзор
Электрон-вольт, обозначаемый как эВ, а иногда и как электронвольт, — это единица энергии, используемая в физике элементарных зарядов и электричества.
Электрон-вольт определяется как количество энергии, полученной или потерянной зарядом электрона, перемещающегося через разность электрических потенциалов в один вольт. Таким образом, он равен произведению одного вольта (1 Дж / Кл) на один элементарный заряд, что дает ему значение в джоулях, приблизительно равное 1,602 × 10 -19 Дж.
Электрон-вольт сам по себе не является единицей СИ, он стал полезен в результате экспериментов. Ученые, работающие с электростатическими ускорителями частиц, обычно использовали соотношение между энергией (E), зарядом (q) и разностью потенциалов (V) в своей работе:
[латекс] \ text {E} = \ text {qV} [/ latex]
Все вычисления энергии по приведенному выше уравнению были квантованы как кратные элементарному заряду q для данного напряжения, и, таким образом, возникло обычное использование электрон-вольт в качестве единицы измерения.
Импульс
Электрон-вольт и импульс являются мерой энергии, и они связаны между собой в физике высоких энергий. Приложение разности потенциалов к электрону дает ему энергию, которая проявляется в движении электрона через него. Учитывая, что у электрона есть масса и скорость, у него есть импульс. Деление электрон-вольт на константу с единицами измерения скорости дает импульс.
Масса
Учитывая, что масса эквивалентна энергии, электрон-вольт может измерять массу.2} [/ латекс]
Длина волны
Энергия E , частота v и длина волны λ фотона связаны соотношением
[латекс] \ text {E} (\ text {eV}) = \ text {hv} = \ frac {\ text {hc}} {\ lambda} [/ latex]
где h — постоянная Планка, c — скорость света. Таким образом, фотон с длиной волны 532 нм (зеленый свет) будет иметь энергию примерно 2,33 эВ. Точно так же 1 эВ соответствует инфракрасному фотону с длиной волны 1240 нм и так далее.
Энергия фотонов в видимом спектре : Связь между длиной волны и энергией, выраженная в электрон-вольтах.
Температура
В физике плазмы электрон-вольт может использоваться как единица измерения температуры. Чтобы преобразовать в Кельвины, просто разделите значение 1 эВ (в Джоулях) на постоянную Больцмана (1,3806505 (24) × 10 -23 Дж / К).
Дипольные моменты
Электрический дипольный момент — это мера полярности в системе.
Цели обучения
Свяжите электрический дипольный момент с полярностью в системе
Основные выводы
Ключевые моменты
- Электрические дипольные моменты используются для измерения разделения положительных и отрицательных зарядов (полярности) в системе. Они измеряются в кулонах-метрах (Км).
- Для точечных зарядов со значениями + q и -q электрический дипольный момент (p) может быть определен как: [latex] \ text {p} = \ text {qd} [/ latex], где q представляет собой заряды, а d представляет собой вектор смещения.Вектор смещения имеет величину расстояния между зарядами и направление от отрицательного заряда к положительному.
- Все диполи испытывают крутящий момент, который вращает диполь, выравнивая его с электрическим полем. Этот крутящий момент можно рассчитать как произведение электрического дипольного момента и электрического поля.
Ключевые термины
- дипольный момент : векторное произведение заряда на любом полюсе диполя на расстояние, разделяющее их.
- вектор : направленная величина, имеющая как величину, так и направление; между двумя точками.
- крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)
Электрический дипольный момент — это мера полярности, которая представляет собой разделение положительных и отрицательных зарядов в системе. Он измеряется в кулонах-метрах (Км). Существует много различных типов дипольных моментов, включая электрические дипольные моменты, магнитные дипольные моменты и топологические дипольные моменты.
К подмножеству электрических дипольных моментов относятся дипольные моменты переходов, дипольные моменты молекул, дипольные моменты связей и электрические дипольные моменты электронов. Для целей этого атома мы сосредоточимся на широком обзоре электрического дипольного момента в статических ситуациях.
Молекулярный дипольный момент в воде : Эта молекула воды (H 2 O) имеет высокую плотность электронов (обозначена красной штриховкой) около красного атома O. Ближе к белым атомам H наблюдается малая плотность электронов.Следовательно, молекула является диполем, с отрицательностью около O и положительностью ближе к атомам H.
Определение
По сути, для случая точечных зарядов со значениями + q и -q электрический дипольный момент (p) может быть определен как векторное произведение зарядов и вектора смещения d:
[латекс] \ text {p} = \ text {qd} [/ latex]
Вектор смещения — это вектор с величиной, равной расстоянию между зарядами, и направлением, указывающим от отрицательного заряда к положительному.По сути, он взаимозаменяем с переменной «радиус» во многих других уравнениях (например, в тех, которые определяют гравитационные и электростатические силы), за исключением того, что он включает фактор направления.
Крутящий момент
Все диполи испытывают крутящую силу или крутящий момент, когда они помещаются во внешние электрические поля. Этот крутящий момент вращает диполь, чтобы выровнять его с полем. Это вызвано необходимостью минимизировать потенциальную энергию. Крутящий момент (τ) можно рассчитать как произведение электрического дипольного момента и электрического поля (E), предполагая, что E пространственно однородно:
[латекс] \ tau = \ text {p} \ times \ text {E} [/ latex]
Электрическая потенциальная энергия: разница потенциалов
Цели обучения
К концу этого раздела вы сможете:
- Определите электрический потенциал и электрическую потенциальную энергию.
- Опишите взаимосвязь между разностью потенциалов и электрической потенциальной энергией.
- Объясните электрон-вольт и его использование в субмикроскопических процессах.
- Определите электрическую потенциальную энергию по разности потенциалов и количеству заряда.
Рис. 1. Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма. В обоих случаях потенциальная энергия преобразуется в другую форму. Работа совершается силой, но поскольку эта сила консервативна, мы можем записать W = –ΔPE.
Когда свободный положительный заряд q ускоряется электрическим полем, как показано на рисунке 1, ему придается кинетическая энергия. Этот процесс аналогичен ускорению объекта гравитационным полем. Это как если бы заряд спускался с электрического холма, где его электрическая потенциальная энергия преобразуется в кинетическую. Давайте исследуем работу, совершаемую электрическим полем над зарядом q в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.
Электростатическая или кулоновская сила является консервативной, что означает, что работа, выполняемая на q , не зависит от пройденного пути. Это в точности аналог гравитационной силы в отсутствие диссипативных сил, таких как трение. Когда сила является консервативной, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией (потому что она зависит только от положения), чем вычислять работу напрямую.
Мы используем буквы PE для обозначения электрической потенциальной энергии, которая измеряется в джоулях (Дж). Изменение потенциальной энергии ΔPE имеет решающее значение, поскольку работа, совершаемая консервативной силой, является отрицательной по отношению к изменению потенциальной энергии; то есть W = –ΔPE. Например, работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы значение W было положительным.PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.
Потенциальная энергия
W = –ΔPE. Например, работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы значение W было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.
Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное понимание энергии и преобразования энергии без необходимости иметь дело с силой напрямую. Например, гораздо более распространено использование концепции напряжения (связанного с электрической потенциальной энергией), чем непосредственное рассмотрение кулоновской силы.
Непосредственный расчет работы обычно затруднен, так как W = Fd cos θ , а направление и величина F могут быть сложными для нескольких зарядов, для объектов неправильной формы и вдоль произвольных траекторий.Но мы знаем, что, поскольку F = qE , работа и, следовательно, ΔPE пропорциональны испытательному заряду q. Чтобы получить физическую величину, не зависящую от пробного заряда, мы определяем электрический потенциал V (или просто потенциал, поскольку подразумевается электрический) как потенциальную энергию на единицу заряда [латекс] V = \ frac {\ text {PE}} {q} \\ [/ латекс].
Электрический потенциал
Это электрическая потенциальная энергия на единицу заряда.
[латекс] \ displaystyle {V} = \ frac {\ text {PE}} {q} \\ [/ latex]
Поскольку PE пропорционален q , зависимость от q отменяется. Таким образом, V не зависит от q . Изменение потенциальной энергии ΔPE имеет решающее значение, поэтому нас беспокоит разность потенциалов или разность потенциалов Δ V между двумя точками, где
[латекс] \ displaystyle \ Delta {V} = V _ {\ text {B}} — V _ {\ text {A}} = \ frac {\ Delta {\ text {PE}}} {q} \\ [/ латекс]
Таким образом, разность потенциалов между точками A и B, V B — V A , определяется как изменение потенциальной энергии заряда q , перемещенное от A к B, делится на заряд.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.
[латекс] 1 \ text {V} = 1 \ frac {\ text {J}} {\ text {C}} \\ [/ latex]
Возможная разница
Разность потенциалов между точками A и B, V B — V A , определяется как изменение потенциальной энергии заряда q , перемещенного от A к B, деленное на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.
[латекс] \ displaystyle {1} \ text {V} = 1 \ frac {\ text {J}} {\ text {C}} \\ [/ latex]
Знакомый термин напряжение — это общее название разности потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, а ее напряжение — это разность потенциалов между ними. По сути, точка, которую вы выбираете равным нулю вольт, произвольна. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например, на уровне моря или, возможно, на полу лекционного зала.
Таким образом, связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением [латекс] \ Delta {V} = \ frac {\ Delta \ text {PE}} {q} \\ [/ latex] и ΔPE = q Δ V .
Разница потенциалов и электрическая потенциальная энергия
Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой
.[латекс] \ Delta {V} = \ frac {\ Delta \ text {PE}} {q} \\ [/ latex] и ΔPE = q Δ V
Второе уравнение эквивалентно первому.
Напряжение — это не то же самое, что энергия. Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между выводами аккумулятора), но один хранит гораздо больше энергии, чем другой, поскольку ΔPE = q Δ V . Автомобильный аккумулятор может заряжаться больше, чем аккумулятор мотоцикла, хотя оба аккумулятора — 12 В.
Пример 1. Расчет энергии
Предположим, у вас есть 12.Батарея мотоцикла 0 В, способная перемещать заряд 5000 C, и автомобильная батарея 12,0 В, способная перемещать заряд 60 000 C. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда соответствует трем значащим цифрам.)
Стратегия
Сказать, что у нас батарея 12,0 В, означает, что ее клеммы имеют разность потенциалов 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное ΔPE = q Δ V .
Итак, чтобы найти выходную энергию, мы умножаем перемещенный заряд на разность потенциалов.
Решение
Для аккумулятора мотоцикла: q = 5000 C и Δ V = 12,0 В. Общая энергия, отдаваемая аккумулятором мотоцикла, составляет
[латекс] \ begin {array} {lll} \ Delta \ text {PE} _ {\ text {cycle}} & = & \ left (5000 \ text {C} \ right) \ left (12.0 \ text {V } \ right) \\\ text {} & = & \ left (5000 \ text {C} \ right) \ left (12.0 \ text {J / C} \ right) \\\ text {} & = & 6.5 \ text {J} \ end {array} \\ [/ latex]
Обсуждение
Хотя напряжение и энергия связаны, это не одно и то же. Напряжения батарей одинаковы, но энергия, подаваемая каждым из них, совершенно разная. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за низкого заряда автомобильного аккумулятора. Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.
Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд — в частности, электроны. Батареи отталкивают электроны от своих отрицательных выводов (A) через любую задействованную схему и притягивают их к своим положительным выводам (B), как показано на рисунке 2. Изменение потенциала составляет Δ В = В B — V A = +12 В и заряд q отрицательный, так что ΔPE = q Δ V отрицательный, что означает, что потенциальная энергия аккумулятора уменьшилась, когда q переместился из От А до Б.
Рис. 2. Батарея перемещает отрицательный заряд от отрицательной клеммы через фару к ее положительной клемме. Соответствующие комбинации химикатов в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается избыточным положительным зарядом на другом выводе. С точки зрения потенциала положительный вывод находится под более высоким напряжением, чем отрицательный. Внутри аккумулятора движутся как положительные, так и отрицательные заряды.
Пример 2. Сколько электронов проходит через фару каждую секунду?
Когда от автомобильного аккумулятора на 12,0 В работает одна фара мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?
Стратегия
Чтобы узнать количество электронов, мы должны сначала найти заряд, который переместился за 1,00 с. Перемещаемый заряд связан с напряжением и энергией посредством уравнения ΔPE = q Δ V . Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, имеем ΔPE = –30.0 Дж, и, поскольку электроны переходят от отрицательного вывода к положительному, мы видим, что Δ V = + 12.0V.
Решение
Чтобы найти заряд q перемещенный, мы решаем уравнение ΔPE = q Δ V : [latex] q = \ frac {\ Delta \ text {PE}} {\ Delta {V}} \ \[/латекс].
Вводя значения ΔPE и Δ V , получаем
[латекс] q = \ frac {-30.0 \ text {J}} {+ 12.0 \ text {V}} = \ frac {-30.0 \ text {J}} {+ 12.0 \ text {J / C}} — 2.{19} \ text {электроны} \\ [/ latex]
Обсуждение
Это очень большое количество. Неудивительно, что мы обычно не наблюдаем отдельные электроны, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными. Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.
Электрон вольт
Рис. 3. Типичная электронная пушка ускоряет электроны с помощью разности потенциалов между двумя металлическими пластинами. Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны 5000 эВ.
Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение.Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать вредные рентгеновские лучи, которые также могут нанести ущерб. Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам. На рисунке 3 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели.Электрону придается кинетическая энергия, которая позже преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что спуск для электрона — это подъем для положительного заряда.) Поскольку энергия связана с напряжением соотношением ΔPE = q Δ V , мы можем рассматривать джоуль как кулон-вольт.
В субмикроскопическом масштабе удобнее определять единицу энергии, называемую электрон-вольт (эВ), которая представляет собой энергию, отдаваемую фундаментальному заряду, ускоренному через разность потенциалов в 1 В.{-19} \ text {J} \ end {array} \\ [/ latex]
Электрону, ускоренному через разность потенциалов 1 В, придается энергия 1 эВ. Отсюда следует, что электрону, ускоренному до 50 В, дается 50 эВ. Разность потенциалов 100 000 В (100 кВ) даст электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получит энергию 200 эВ. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.
Установление соединений: единицы энергии
Электрон-вольт (эВ) — наиболее распространенная единица измерения энергии для субмикроскопических процессов. Особенно это будет заметно в главах, посвященных современной физике. Энергия настолько важна для столь многих предметов, что существует тенденция определять специальные единицы энергии для каждой основной темы. Есть, например, калории для пищевой энергии, киловатт-часы для электроэнергии и термы для энергии природного газа.
Электрон-вольт обычно используется в субмикроскопических процессах — химические валентные энергии, молекулярные и ядерные энергии связи входят в число величин, часто выражаемых в электрон-вольтах.Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, ему дается энергия 30 кэВ (30 000 эВ), и он может разрушить до 6000 этих молекул (30 000 эВ ÷ 5 эВ на молекулу = 6000 молекул. ). Энергия ядерного распада составляет порядка 1 МэВ (1000000 эВ) на событие и, таким образом, может нанести значительный биологический ущерб.
Сохранение энергии
Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) работы или теплопередачи.Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.
Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы; то есть KE + PE = константа. Потеря ПЭ заряженной частицы становится увеличением ее КЭ. Здесь PE — электрическая потенциальная энергия. Сохранение энергии выражается в форме уравнения как KE + PE = константа или KE i + PE i = KE f + PE f , где i и f обозначают начальные и конечные условия.Как мы уже много раз выясняли, учет энергии может дать нам понимание и облегчить решение проблем.
Пример 3. Электрическая потенциальная энергия, преобразованная в кинетическую энергию
Рассчитайте конечную скорость свободного электрона, ускоренного из состояния покоя через разность потенциалов 100 В. (Предположим, что это числовое значение имеет точность до трех значащих цифр).
Стратегия
У нас есть система, в которой действуют только консервативные силы. Предполагая, что электрон ускоряется в вакууме, и пренебрегая гравитационной силой (мы проверим это предположение позже), вся электрическая потенциальная энергия преобразуется в кинетическую энергию.6 \ text {m / s} \ end {array} \\ [/ latex]
Обсуждение
Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на рисунке 3. Из обсуждений в разделе «Электрический заряд и электрическое поле» мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны с помощью малых напряжений из-за их очень малой массы.В электронных пушках обычно используются напряжения, намного превышающие 100 В. Эти более высокие напряжения вызывают настолько большие скорости электронов, что необходимо учитывать релятивистские эффекты. Вот почему в этом примере рассматривается (точно) низкое напряжение.
Сводка раздела
- Электрический потенциал — это потенциальная энергия на единицу заряда.
- Разность потенциалов между точками A и B, V B — V A , определяемая как изменение потенциальной энергии заряда q , перемещенного от A к B, равна изменению потенциальная энергия, деленная на заряд. Разность потенциалов обычно называется напряжением и обозначается символом Δ V : [латекс] \ Delta V = \ frac {\ Delta \ text {PE}} {q} \\ [/ латекс] и ΔPE = q Δ V .{\ text {-19}} \ text {J.} \ end {array} \\ [/ latex]
- Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы, то есть KE + PE. Эта сумма постоянна.
Концептуальные вопросы
- Напряжение — это обычное слово для обозначения разности потенциалов. Какой термин является более описательным, напряжение или разность потенциалов?
- Если напряжение между двумя точками равно нулю, можно ли перемещать тестовый заряд между ними при нулевой работе сети? Обязательно ли это делать без применения силы? Объяснять.
- Какая связь между напряжением и энергией? Точнее, какова взаимосвязь между разностью потенциалов и электрической потенциальной энергией?
- Напряжение всегда измеряется между двумя точками. Почему?
- Как связаны единицы вольт и электронвольт? Чем они отличаются?
Задачи и упражнения
- Найдите отношение скоростей электрона и отрицательного иона водорода (тот, у которого есть дополнительный электрон), ускоренных одним и тем же напряжением, принимая нерелятивистские конечные скорости.Возьмем массу иона водорода 1,67 × 10 −27 кг.
- В вакуумированной трубке используется ускоряющее напряжение 40 кВ для ускорения электронов, ударов по медной пластине и получения рентгеновских лучей. С нерелятивистской точки зрения, какова максимальная скорость этих электронов?
- Голое ядро гелия имеет два положительных заряда и массу 6,64 × 10 −27 кг. (а) Вычислите его кинетическую энергию в джоулях при 2,00% скорости света. (б) Что это в электрон-вольтах? (c) Какое напряжение потребуется для получения этой энергии?
- Интегрированные концепции. Однозарядные ионы газа ускоряются из состояния покоя за счет напряжения 13,0 В. При какой температуре средняя кинетическая энергия молекул газа будет такой же, как у этих ионов?
- Интегрированные концепции. Считается, что температура около центра Солнца составляет 15 миллионов градусов Цельсия (1,5 × 10 7 ºC). Через какое напряжение должен быть ускорен однозарядный ион, чтобы он имел такую же энергию, как средняя кинетическая энергия ионов при этой температуре?
- Интегрированные концепции. (a) Какова средняя выходная мощность дефибриллятора сердца, который рассеивает 400 Дж энергии за 10,0 мс? (б) Учитывая высокую выходную мощность, почему дефибриллятор не вызывает серьезных ожогов?
- Интегрированные концепции. Молния поражает дерево, перемещая 20,0 Кл заряда через разность потенциалов 1,00 × 10 2 МВ. а) Какая энергия была рассеяна? б) Какую массу воды можно было поднять с 15ºC до точки кипения, а затем с помощью этой энергии вскипятить? (c) Обсудите ущерб, который может быть нанесен дереву из-за расширения кипящего пара.
- Интегрированные концепции. Подогреватель бутылочек на 12,0 В нагревает 50,0 г стекла, 2,50 × 10 2 г детской смеси и 2,00 × 10 2 г алюминия с 20,0 ° C до 90,0 ° C. (а) Насколько заряжен аккумулятор? (б) Сколько электронов течет в секунду, если для разогрева формулы требуется 5,00 мин? (Подсказка: предположите, что удельная теплоемкость детской смеси примерно такая же, как удельная теплоемкость воды.)
- Интегрированные концепции. В автомобиле с батарейным питанием используется 12.Система 0 В. Найдите заряд, который батареи должны быть в состоянии двигаться, чтобы разогнать 750-килограммовый автомобиль из состояния покоя до 25,0 м / с, заставить его подняться на холм высотой 2,00 × 10 2 м, а затем заставить его двигаться с постоянной скоростью 25,0 м / с. м / с путем приложения силы 5,00 × 10 2 Н в течение часа.
- Интегрированные концепции. Вероятность слияния значительно увеличивается, когда соответствующие ядра сближаются, но взаимное кулоновское отталкивание должно быть преодолено. Это можно сделать, используя кинетическую энергию ионов высокотемпературного газа или ускоряя ядра друг к другу.(а) Вычислите потенциальную энергию двух однозарядных ядер, разделенных расстоянием 1,00 × 10 −12 м, найдя напряжение одного на таком расстоянии и умножив его на заряд другого. (б) При какой температуре атомы газа будут иметь среднюю кинетическую энергию, равную этой необходимой электрической потенциальной энергии?
- Необоснованные результаты. (a) Найдите напряжение около металлической сферы диаметром 10,0 см, на которой имеется 8,00 C избыточного положительного заряда. б) Что неразумного в этом результате? (c) Какие допущения ответственны?
- Создайте свою проблему. Рассмотрим аккумулятор, используемый для питания сотового телефона. Постройте задачу, в которой вы определяете энергию, которая должна быть предоставлена аккумулятором, а затем вычисляете количество заряда, которое он должен иметь возможность перемещать, чтобы обеспечить эту энергию. Среди прочего следует учитывать потребность в энергии и напряжение батареи. Возможно, вам придется заглянуть в будущее, чтобы интерпретировать номинальные характеристики батареи в ампер-часах производителя как энергию в джоулях.
Глоссарий
электрический потенциал: потенциальная энергия на единицу заряда
разность потенциалов (или напряжение): изменение потенциальной энергии заряда, перемещенного из одной точки в другую, деленное на заряд; единицы разности потенциалов — джоули на кулон, известные как
вольт.электрон-вольт: энергия, отданная фундаментальному заряду, ускоренному через разность потенциалов в один вольт
механическая энергия: сумма кинетической энергии и потенциальной энергии системы; эта сумма является постоянной
Избранные решения проблем и упражнения
1.


 {\displaystyle z=\sum _{j}\mu _{j}\mathrm {d} m_{j}=\mathrm {d} E-q-w=\mathrm {d} E-T\mathrm {d} S+P\mathrm {d} V.}
{\displaystyle z=\sum _{j}\mu _{j}\mathrm {d} m_{j}=\mathrm {d} E-q-w=\mathrm {d} E-T\mathrm {d} S+P\mathrm {d} V.} Теория и задачи механики сплошных сред. — М.: Мир, 1974. — 319 с.
Теория и задачи механики сплошных сред. — М.: Мир, 1974. — 319 с.

 Для этого необходимы специальные приборы.
Для этого необходимы специальные приборы. 10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.
10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.