Сила Лоренца – формула, величина, примеры кратко определение и как определить направление

4.7

Средняя оценка: 4.7

Всего получено оценок: 349.

4.7

Средняя оценка: 4.7

Всего получено оценок: 349.

На проводник с током в магнитном поле действует сила Ампера. Однако магнитное поле способно взаимодействовать и с отдельными электрическими зарядами. Рассмотрим кратко эту тему, узнаем, как определить направление и величину силы, действующей на заряд в магнитном поле.

Взаимодействие магнитного поля с зарядами

Опыты показывают, что магнитное поле никак не влияет на покоящийся электрический заряд. Почему же магнитное поле взаимодействует с проводником с электрическим током, который представляет собой движущиеся электрические заряды ?

Причина в движении зарядов. Магнитное поле не взаимодействует с зарядом, пока его скорость в этом поле равна нулю. Однако, как только заряд начинает двигаться, сразу же возникает сила, направленная перпендикулярно вектору скорости заряда.

Это приводит к интересному результату. Из механики известно, что если материальная точка движется под действием силы, направленной перпендикулярно вектору скорости, то ее траектория представляет собой окружность. Именно это и происходит с движущимися заряженными частицами в однородном магнитном поле. Заряженные частицы под действием магнитного поля движутся по окружностям.

Рис. 1. Движение заряженной частицы в магнитном поле.

Сила Лоренца

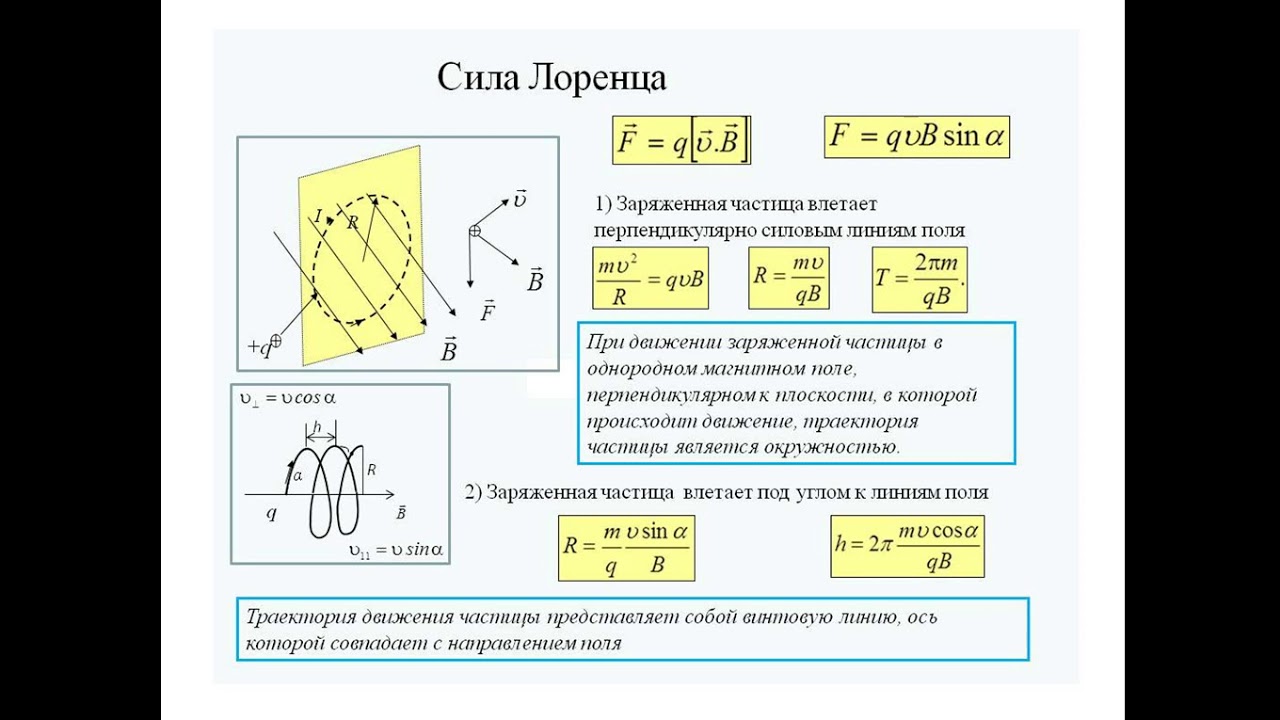
Сила, которая возникает при движении заряда в магнитном поле, называется силой Лоренца. Именно силы Лоренца, действующие на отдельные заряды в проводнике, приводят к появлению общей силы Ампера. Поэтому формулу силы Лоренца можно получить из закона Ампера.

Сила Ампера равна:

$$F_A= IB Δl sin \alpha$$

Величина тока, идущая в проводнике, прямо пропорциональна величине заряда носителей $q$, их концентрации $n$, скорости их движения $v$ и площади поперечного сечения проводника $S$:

$$I = qnvS$$

Подставляя это выражение в предыдущую формулу, получим:

$$ F_A = qnvSBΔl sin \alpha$$

Сила Ампера действует на проводник в результате сложения сил Лоренца, действующих на каждый из зарядов в проводнике.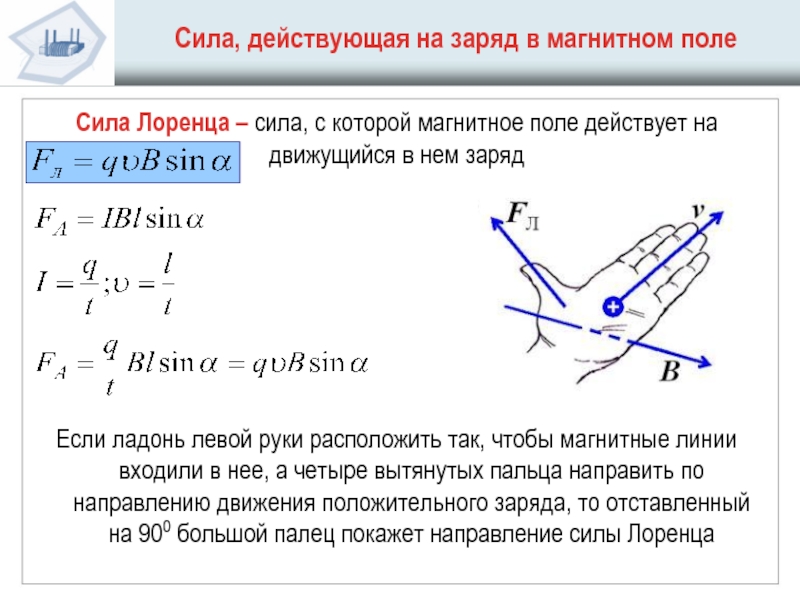 То есть для получения силы Лоренца, действующей на отдельный носитель, надо величину силы Ампера поделить на число носителей. Число носителей $N$ равно произведению концентрации носителей на объем проводника:

$$N=nSΔl$$

Следовательно, сила Лоренца равна:

$$F_L = {F_A \over N}= qvB sin \alpha$$

Как и в случае силы Ампера, угол $\alpha $ — это угол между направлением движения носителя заряда (вектором скорости) и вектором магнитной индукции.

Направление силы Лоренца определяется точно так же, как и направление силы Ампера: с помощью мнемонического правила левой руки. Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения положительного заряда (против направления для отрицательного), а перпендикулярная составляющая индукции $B_{\perp}$ входила в ладонь, то большой палец покажет направление силы Лоренца.

Рис. 2. Правило левой руки.

Получается, что сила Лоренца всегда направлена перпендикулярно движению заряженной частицы. А это значит, что сила Лоренца не совершает работу и, следовательно, не меняет кинетическую энергию частицы. Она меняет лишь направление ее движения.

Примером использования силы Лоренца является отклоняющая система кинескопов. Отклоняющие системы в телевизорах с кинескопами представляют собой электрические катушки, создающие меняющееся магнитное поле. Под действием этого поля на электроны, вылетающие из электронной пушки, начинает действовать сила Лоренца, они отклоняются и направляются в нужную в данный момент точку экрана.

Рис. 3. Отклоняющая система кинескопа.

Что мы узнали?

Сила Лоренца — это сила, действующая со стороны магнитного поля на движущийся электрический заряд. Сила Лоренца направлена перпендикулярно скорости движения частицы, и для определения этого направления используется правило левой руки. В однородном магнитном поле траектории заряженных частиц, движущихся под действием силы Лоренца, представляют собой окружности.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 349.

---

А какая ваша оценка?

XI. Сила лоренца

1. Электрон, пройдя ускоряющую разность потенциалов U=400В, попал в однородное магнитное поле с индукцией В=1,5мТл. Определить: 1) радиус кривизны траектории; 2) частоту n вращения электрона в магнитном поле. Вектор скорости электрона перпендикулярен линиям индукции.

2. Электрон влетает в однородное магнитное поле напряженностью Н=16кА/м со скоростью 8Мм/с. Вектор скорости составляет угол

   =60 с направлением линий индукции. Определить радиус R и шаг h винтовой линии, по которой будет двигаться электрон в магнитном поле.

3. Электрон движется в однородном магнитном поле напряженностью Н=4кА/м со скоростью V=10Мм/с. Вектор скорости направлен перпендикулярно линиям напряженности. Найти силу F, с которой поле действует на электрон, и радиус R окружности, по которой он движется.

4. Электрон движется в однородном магнитном поле с индукцией

   В=0,1Тл перпендикулярно линиям индукции. Найти силу F, с которой поле действует на электрон, если радиус R окружности, по которой он движется, равен 0,5см.

5. Двукратно ионизированный атом гелия (-частица) движется в однородном магнитном поле напряженностью Н=100кА/м по окружности радиусом 10см. Найти скорость V -частицы.

6. Вычислить радиус R дуги окружности, которую описывает электрон в магнитном поле с индукцией В=15мТл, если скорость электрона равна 2Мм/с.

7. Заряженная частица с энергией Т=1кэВ движется в однородном магнитном поле по окружности радиусом 1мм . Найти силу, действующую на частицу со стороны поля.

8. Заряженная частица, пройдя ускоряющую разность потенциалов U=2кВ, попав в однородное магнитное поле с индукцией В=15,1мТл, движется по окружности радиусом 1мм. Определить отношение q /m заряда частицы к ее массе и скорость V частицы.

9. Заряженная частица, обладающая скоростью V

   =2•10⁶м/с, влетела в однородное магнитное поле с индукцией В=0,52Тл. Найти отношение Q/m заряда частицы к ее массе, если частица в поле описала дугу окружности радиусом 4см. По этому отношению определить, какая это частица.

10. Протон, пройдя ускоряющую разность потенциалов U=600В, движется в однородном магнитном с индукцией В=0,3Тл по окружности. Вычислить ее радиус.

11. Поток -частиц, ускоренных разностью потенциалов U=1МВ, влетает в однородное магнитное поле напряженностью Н=1,2кА/м.

    Скорость каждой частицы направлена перпендикулярно к направлению магнитного поля. Найти силу F, действующую на каждую частицу.

12. Электрон влетает в однородное магнитное поле, направление которого перпендикулярно к направлению его движения. Скорость электрона V=4•10⁷м/с. Индукция магнитного поля В=1мТл. Найти тангенциальное и нормальное ускорения электрона в магнитном поле.

13. Протон и электрон, двигаясь с одинаковой скоростью, влетают в однородное магнитное поле. Во сколько раз радиус кривизны

    R₁ траектории протона больше радиуса кривизны R₂ траектории электрона?

14. Протон и -частица влетают в однородное магнитное поле, направление которого перпендикулярно к направлению их движения. Во сколько раз период обращения Т₁ протона в магнитном поле больше периода обращения Т₂ -частицы?

15. -частица, кинетическая энергия которой W=500эВ, влетает в однородное магнитное поле, перпендикулярное к направлению ее движения.

    Индукция магнитного поля В=0,1Тл. Найти силу F, действующую на -частицу, радиус R окружности, по которой движется -частица, и период обращения Т -частицы.

16. Найти отношение q/m для заряженной частицы, если она, влетая со скоростью V=10⁶м/с в однородное магнитное поле напряженностью Н=200кА/м, движется по дуге окружности радиусом R=8,3см. Направление скорости движения частицы перпендикулярно к направлению магнитного поля. Сравнить найденное значение со значением q/m для электрона, протона и -частицы.

17. Электрон, ускоренный разностью потенциалов U=6кВ, влетает в однородное магнитное поле под углом =30 к направлению поля и движется по винтовой траектории. Индукция магнитного поля В=13мТл. Найти радиус R и шаг h винтовой траектории.

18. Протон влетает в однородное магнитное поле под углом =30 к направлению поля и движется по винтовой линии радиусом R=1,5см. Индукция магнитного поля В=0,1Тл. Найти кинетическую энергию W протона.

19. Электрон, обладая скоростью V=10Мм/с, влетел в однородное магнитное поле перпендикулярно линиям магнитной индукции. Индукция магнитного поля В=0,1мТл. Определить нормальное и тангенциальное ускорения электрона.

20. В однородном магнитном поле перпендикулярно линиям магнитной индукции движется прямой проводник длиной 40см. Определить силу Лоренца, действующую на свободный электрон проводника, если возникающая на его концах разность потенциалов составляет 10мкВ.

21. Электрон, ускоренный разностью потенциалов U=0,5кВ, движется параллельно прямолинейному длинному проводнику на расстоянии r=1см от него. Определить силу, действующую на электрон, если через проводник пропускать ток I=10А.

22. Протон, пройдя ускоряющую разность потенциалов U=0,5кВ, движется в однородном магнитном с индукцией В=2мТл по окружности. Вычислить ее радиус.

23. Электрон влетает в однородное магнитное поле с магнитной индукцией В=0,2мТл под углом =30 к направлению поля и движется по винтовой линии. Определить скорость электрона, если радиус винтовой линии R=3см, а шаг h=9см.

24. Определить напряженность Н поля, создаваемого прямолинейно равномерно движущимся со скоростью V=5000км/с электроном в точке, находящейся от него на расстоянии r=10нм и лежащей на перпендикуляре к вектору V, проходящем через мгновенное положение электрона.

25. Электрон движется прямолинейно с постоянной скоростью V=0,2Мм/с. Определить магнитную индукцию В поля, создаваемого электроном в точке, находящейся на расстоянии r=2нм от электрона и лежащей на прямой, проходящей через мгновенное положение электрона и составляющей угол =45 со скоростью движения электрона.

26. Винтовая линия, по которой движется электрон в однородном магнитном поле, имеет диаметр 80мм и шаг 200мм. Индукция поля В=0,03Тл. Определить скорость электрона.

27. В пространстве в отсутствии силы тяжести имеются параллельные вертикальные электрическое (Е=10В/м) и магнитное поля (В=3Тл). Шарик с положительным зарядом, подвешенный на нити, отклонили на расстояние 2м от оси вращения и толкнули со скоростью 5м/с так, что он стал описывать окружность. Нить отклонена на угол 45^о от оси. Найти отношение заряда шарика к его массе.

28. Электроны вылетают из электронной пушки, пройдя ускоряющее напряжение 10⁵В. Какова должна быть индукция однородного магнитного поля, перпендикулярного движению электронов, чтобы вылетающие из пушки электроны попадали в мишень, расположенную на расстоянии 1м от отверстия пушки под углом 30^о к направлению скорости вылетающих электронов.

29. Электрон влетает в однородное магнитное поле с индукцией 10 ^-3Тл перпендикулярно силовым линиям и под углом /4 к границе поля. Скорость электрона 10⁶м/с. В направлении осей X и Y магнитное поле безгранично. На каком расстоянии от точки влета электрон вылетит из поля?

ньютоновская механика — Обнаружение силы реакции на силу Лоренца

спросил 1 год, 4 месяца назад

Изменено 1 год, 4 месяца назад

Просмотрено 198 раз

$\begingroup$

Если заряженная частица отклоняется в магнитном поле под действием какого-либо магнита, есть ли какой-нибудь эксперимент, который показывает (или измеряет) противоположную силу реакции (из-за третьего закона Ньютона) на магнит?

• ньютоновская механика
• электромагнетизм
• силы
• магнитные поля

$\endgroup$

$\begingroup$

Движущийся заряд взаимодействует с внешним магнитом через его магнитный диполь. Чтобы понять это, необходимы некоторые основные понятия:

1. электрон (как представитель зарядов) имеет собственный (постоянно присутствующий) магнитный диполь.
2. магнитное поле магнита со временем не ослабевает (в качестве магнита можно использовать постоянный магнит). Магнит не отдает энергию постоянно заряду, траектория движения которого тем не менее изгибается.
3. энергия, необходимая для отклонения частицы, исходит от движения части. По мере увеличения продолжительности кривизны заряд замедляется. Его траектория движения представляет собой спираль, и заряд остановился в ее центре.
4. отклонение связано с наблюдаемым излучением ЭМ излучения.

Магнитное поле — это что-то вроде катализатора в химии; поле влияет на процесс, но не потребляется в процессе. Как это работает?

Ключ заключается во временном выравнивании магнитного диполя заряда с этим внешним магнитным полем вместе с одновременным излучением электромагнитного излучения.
Как известно, у ЭМ излучения нет массы, но есть момент. Во-первых, именно этот момент испускаемого излучения и является причиной бокового отклонения. Во-вторых, снова нарушается ориентация диполя на внешнее поле. Из-за 1 замедляется заряд, из-за 2 цикл может начаться заново.

Поскольку электромагнитное излучение является причиной отклонения заряда, на магнит не действует противодействующая «противоположная сила реакции (согласно третьему закону Ньютона)». И, подчеркну еще раз, никакого ослабления внешнего магнитного поля.

$\endgroup$

7

$\begingroup$

Если вы говорите о лабораторном макроскопическом магните как об источнике магнитного поля, то для одиночной заряженной частицы, наверное, нет. Сила реакции микроскопическая. Обнаружить силу одиночной заряженной частицы было бы чрезвычайно сложно. Я не скажу, что это невозможно. Можно было бы использовать что-то вроде сверхпроводящего магнита, чтобы весь магнит можно было рассматривать как единое квантовое состояние. Тогда одна заряженная частица могла бы произвести заметное изменение в магните. Но это будет довольно сложный эксперимент.

Для потока заряженных частиц это довольно просто. Когда работает электродвигатель, сила, создаваемая вращающейся частью двигателя, точно уравновешивается силой, создаваемой остальной частью двигателя. Поэтому, когда вы используете вал электродвигателя для вращения чего-либо, остальная часть двигателя должна поддерживаться, чтобы он не вращался в противоположном направлении.

Для одиночной частицы в магнитном поле микроскопического магнита ситуация очень сложная. Безусловно, можно обнаружить отдачу частиц при столкновении с другими частицами. Однако эта ситуация достаточно сложна из-за взаимодействия с участием электрических и, возможно, ядерных сил. Если протон (заряженная частица) отлетает от ядра (источника магнитного поля), происходит отдача ядра. И такую ​​отдачу можно обнаружить и измерить. Однако рассеяние будет происходить не только от заряда, движущегося через магнитное поле. Будут электрические и ядерные силовые эффекты. А магнитное поле ядра — не такая простая вещь, как можно было бы ожидать в небольших участках электродвигателя. Таким образом, разрешение части, связанной с магнитным полем, является сложной задачей.

$\endgroup$

3

$\begingroup$

Сила реакции действует не на магнит (на некотором расстоянии), а на электромагнитное поле прямо в месте нахождения заряженной частицы. Если заряженная частица получает импульс $\Delta {\bf p}$, то локальное электромагнитное поле теряет ровно столько импульса. Скорость этого изменения импульса и есть сила реакции.

Теперь, если электромагнитное поле в целом статично, то оно должно отдавать тот же самый импульс чему-то другому. Что происходит, так это то, что импульс переносится через поле и в конечном итоге достигает того, что действует как граница поля. Границей могут быть, например, дополнительно заряженные частицы или магнитные диполи в твердом материале, таком как постоянный магнит или электромагнит. Таким образом, в этом случае сила реакции в конечном итоге давит на магнит, создающий поле. Эта сила ощущается всякий раз, когда электрический генератор используется, например, для обеспечения электрического тока. Над током совершается работа, а в генераторе есть такие вещи, как вращающиеся магниты. Для большого генератора к этим магнитам нужно приложить значительную силу, чтобы заставить их вращаться! Это происходит на большинстве электростанций мира. Приложенная сила противодействует силе реакции, о которой говорится в вопросе. Его получают из пара высокого давления на газовой или угольной электростанции, или из давления ветра на турбину, или из давления воды на турбину и т. д. Его легко измерить.

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

электромагнетизм — Электрон, путешествующий через гравитационное и магнитное поле

спросил 6 лет, 10 месяцев назад

Изменено 6 лет, 10 месяцев назад

Просмотрено 1к раз

$\begingroup$

Когда электрон движется через магнитное поле, на него действует сила Лоренца. Сила, действующая на электрон, вызывает ускорение, и поэтому испускается циклотронное излучение. После прочтения этого вопроса Энергия электрона, вращающегося в магнитном поле, я понял, что энергия, выделяемая для формирования излучения, должна быть взята из энергии электрона. Энергия будет браться из кинетической энергии электрона относительно магнитного поля. В конце концов электрон станет неподвижным относительно магнитного поля, и сила Лоренца упадет до нуля. 9{-30}$ Ньютонов.

Предположим, что для некоторого периода времени $T$ и гравитационное поле, и магнитное поле совершенно однородны, так что электрон движется прямолинейно с постоянной скоростью. Это означает, что результирующего ускорения нет, и хотя электрон испытывает силу Лоренца, он не испытывает никакого ускорения относительно магнитного поля. Значит ли это, что циклотронного излучения нет и в течение времени $T$ электрон будет двигаться с этой постоянной скоростью, не теряя энергии?

• электромагнетизм
• гравитация
• магнитные поля
• электроны

$\endgroup$

$\begingroup$

Это удивительно сложный вопрос, и я не уверен, что на него существует общепринятый ответ.

Чтобы понять, почему это так, отключите магнитное поле и придайте электрону достаточную скорость, чтобы он оставался на орбите вокруг Земли. Теперь в системе отсчета Земли электрон имеет центростремительное ускорение $r\omega^2$ и, следовательно, должен излучать излучение. Однако в системе отсчета электрон находится в свободном падении и совсем не ускоряется, поэтому он не должен излучать излучение. И получается противоречие, так как обе точки зрения не могут быть правильными. 92$) и, следовательно, должен излучать. Но он не может быть излучающим, иначе мы имеем парадоксальную ситуацию, когда неподвижный электрон излучает, нарушая при этом сохранение энергии.

Этот вопрос подробно рассматривается в ответе Бена Кроуэлла на вопрос «Излучает ли постоянно ускоряющаяся заряженная частица электромагнитное излучение или нет?», хотя, должен признаться, мне неясно, каков именно ответ.

Происхождение проблемы заключается в том, как общая теория относительности описывает движение под действием силы тяжести, и проблема существует с вашим вопросом, потому что вы рассматриваете движение под действием комбинации силы тяжести и магнитного поля. Можно привести правдоподобный аргумент, что в вашем эксперименте электрон должен излучать, но столь же правдоподобный аргумент можно привести и в том, что он не должен излучать.